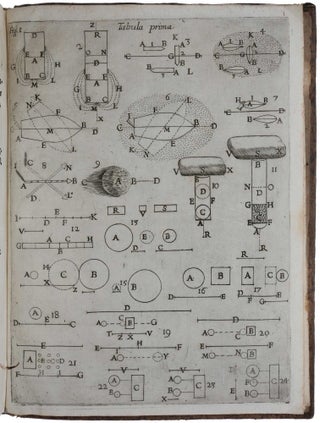
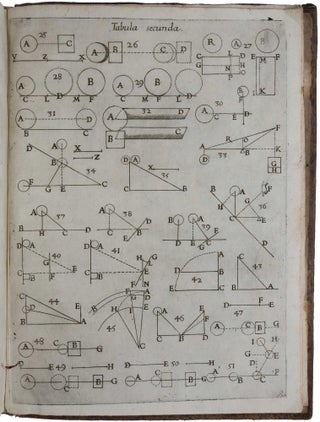
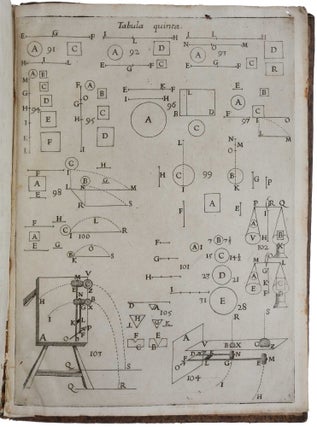
De vi percussionis liber.
Bologna: Giacopo Monti, 1667.
First edition, an extraordinary association copy, of the first published book on the laws of percussion, and containing important hitherto unpublished material from the lectures of Galileo and Torricelli. This copy was a gift from Prince Leopold of Tuscany, Borelli’s patron at the Tuscan court. Probably under the influence of Borelli (see below), Leopold, together with his brother Grand Duke Ferdinand, founded the Accademia del Cimento where Borelli first presented much of the experimental work on which this text is based. Although Leopold held Borelli in high esteem, Borelli’s decision to publish this work in Bologna rather than as part of the proceedings of the Accademia led to a quarrel between the two men. “In this, Borelli’s first book on mechanics, he quotes Galileo’s youthful work on percussion, the fourth Dialogo, and lectures by Torricelli. As well as the detailed discussion of impact, the book deals with the dynamics of falling bodies, vibration, gravity, fluid mechanics, magnetism, and pendular motion … he gives the name resilience for the first time to a number of problems now classed under this name” (Roberts & Trent). This is “the earliest book on the laws of percussion, which undoubtedly influenced John Wallis who, in 1668, published his discovery of the laws governing the percussion of non-elastic bodies, and Christiaan Huygens, who deals with the percussion of elastic bodies in his treatise De motu corporum ex percussion, published in 1669’ (Zeitlinger I, 174). Borelli regarded this work, together with his De motionibus naturalibus (1670), as necessary preparation for his masterpiece, De motum animalium (1680-81), on which he had worked since the early 1660s.
Provenance: Contemporary manuscript ownership entry on half-title dated 4th August 1668 stating that this copy was a gift from Prince Leopold of Tuscany, ‘Dono del Principe Leopoldo de Toscana’, i.e., Cardinal Leopoldo dei Medici (1617-75), scholar, patron of the arts, brother of Ferdinando II, Grand Duke of Tuscany (1610-70).
“In May 1665, Cardinal Michelangelo Ricci, Roman correspondent and adviser to the Tuscan Court, wrote to Borelli’s patron, Leopoldo de Medici, encouraging Borelli to apply himself to the composition of a treatise on motion. According to Ricci, motion was a particularly important topic since so many contemporaries, famed for their contributions to mathematics and philosophy, had dedicated so much time to the topic and had explained so many of nature’s secrets. Borelli’s initial response was that he was instead concentrating on a treatise on anatomy within which he would insert some words regarding collision of moving bodies. At some point in this discussion, seemingly prompted by an insistence from Ricci, Borelli decided to publish On the Force of Percussion independently from his main project. The intention of the book on colliding bodies was to establish crucial propositions concerning motion as a means of introducing issues related to human and animal movements.
“The main problem in question, as Aristotle had put it, was to explain why a heavy axe, as an example, has virtually no effect when rested on a piece of wood but has a much greater impact when it is made to fall from a significant height. Aristotelians believed that the increased force is a result simply of the velocity of the movable; the velocity supposedly artificially increases the weight of the object. For Italian natural philosophers in the seventeenth century, the first point of reference in response to this Aristotelian position is the work carried out by Galileo concerned with motion and mechanics including percussion. In his Mechanics (c. 1590), Galileo claimed that to study percussion, one must consider ‘that which has been seen to happen in all other mechanical operations, which is that the force, the resistance, and the space through which the motion is made respectively follow that proportion and obey those laws by which a resistance equal to the force will be moved by this force through an equal space and with equal velocity to that of the mover.’ That was to say that it is not only the weight of the body in motion that determines the force of percussion but the distance it travels and its velocity before impact that is required to overcome the resistance of the body being impacted upon. Galileo elaborated on his argument in Discourse Concerning Two New Sciences (1638), where he presented several experiments in which the force of percussion was tested and measured by relying on the proportions of opposing forces (including distances and velocities) rather than simply differences in weight.
“In On the Force of Percussion, Borelli agrees with the Galilean proposition that the energies of colliding bodies are not measurable through weight alone. To prove his point, he begins with a series of propositions explaining how a body must be first moved by an impeller in order to acquire a “motive virtue” or “impetus”. Upon colliding with another body at rest, that impetus is transmitted to the stationary body, overcomes its resistance proportional to the mass and velocity of the first body and itself sets in motion. Borelli puts it succinctly: ‘Despite the horror of some Aristotelians for the migration of the motive virtue, it seems certain that part of the virtue or impetus which was concentrated in the impelling body is distributed and expanded in the struck body.’ The ‘distribution and expansion’ of impetus does not mean that the struck body acquires the same speed as the first, ‘impelling’ body, only that the motive virtue is preserved and shared between the two bodies—the reactions of these bodies to the collision is proportional to their respective masses. In sum, the impact of colliding bodies occurs in only a moment, but the result of that instant of time—the cause and effect—is dependent upon proportions of velocity and mass …
“This is a strictly mechanical explanation of moving parts of nature reminiscent of Cartesian natural philosophy, whereby motion is explained by the measurements and properties of bodies in contact with each other. In fact, Borelli is explicit in his mechanistic outlook. He contends that the motive virtue of colliding bodies ‘clearly occurs in similar machines’. He makes this point with particular regard to bodies with elastic, spring-like properties … ‘If indeed thrown against a wall or against a steady racket, a playing ball or a water-skin or a spring or any elastic machine is compressed or bent proportionally to its impetus and percussion. The water-skin then rebounds with a more violent, i.e. doubled, impetus. The compression and bending of the machine is increased, doubled, in so far as the percussive compression is doubled.’ Aside from the allusions to the mechanical properties of nature, the reference here to force resulting from compression is also rather important for our understanding of Borelli’s philosophy of motion as it affords him the possibility of considering the spring-like properties of corpuscles. This is an issue to which he returns in his subsequent book [De motionibus naturalibus]” (Boschiero, pp. xiv-xvi).
Borelli also makes in this work an important contribution to the discussion of the laws of falling bodies (pp. 107-110). “Borelli’s analysis of the trajectory of the falling body, though it is, of course, erroneous, is the best ever made before Hooke and Newton. He is the only one who succeeds in disentangling the purely mathematical point of view from the physical. He is, too, the only man before Hooke who is not dominated and befogged by the traditional conception according to which, whether the Earth moves or stands still, a heavy body has, in any case, to move to the center of the Earth on a perfectly straight line … Borelli continues to explain that the force of an “oblique” percussion is to be measured no by the impetus along the “oblique” path, but only by that on the perpendicular, which, he adds, enables us to dispose of the argument proposed some time ago by a celebrated author (Borelli does not name Riccioli) according to whom, if the Earth moved, the motion of a body falling from the top of a tower would be uniform, and, therefore, the force of percussion would not increase, at least not perceptibly, with the increase of the altitude of the fall. The celebrated author forgets, Borelli explains, that the point or plane of impact does not stand still in world-space, but is transported together with the tower and the body falling from its top” (Koyré, pp. 358-60).
In Chapter 25, Borelli gives a discussion of magnetism thought to be based upon a short treatise by Benedetto Castelli entitled Discorso sopra la calamita, which was discovered in manuscript form among some papers by Galileo in the eighteenth century and eventually published in 1883. This treatise is important as the first example of a theory of magnetism which uses elementary magnets to account for magnetization of iron. The main modification introduced by Borelli is the introduction of a magnetic effluvia or vapour from the loadstone to replace Castelli’s propagation of magnetism through the air. Borelli explains magnetization of iron by supposing that “one must postulate that in the iron there are innumerable active and spirited particles. These particles, however, are disposed in a very confused manner, all intertwined in a variety of ways so that not all their Northern poles point in the same direction but are all confusedly mixed...it is necessary to imagine that when the iron is brought near the loadstone and within its sphere, which stems from the exhalation of the vapour of the loadstone, just as by the process of stirring up, the magnetic particles which are within the interstices of the iron are stirred up and turned, and once loosened and set free … they direct their poles in proper orientation toward the pole of the loadstone.” This is not exactly Castelli’s theory, but Borelli borrowed Castelli’s ideas and combined them with the currently prevailing magnetic theories.
Born in Naples, Giovanni Borelli (1608-79) studied mathematics at Rome under Benedetto Castelli. Sometime before 1640 he was appointed professor of mathematics at Messina. In the early 1640s, he met Galileo in Florence. In 1656 Borelli was appointed to the chair of mathematics at the University of Pisa, a post previously held by Galileo. It was in Pisa that Borelli met the Italian anatomist Marcello Malpighi; the two men became founder members of the short-lived Accademia del Cimento. Motivated by Malpighi’s own studies, Borelli began his first investigations into the science of animal movement. This began an interest that would continue for the rest of his life, eventually earning him the title of the Father of Biomechanics.
“One year after Borelli arrived in Tuscany the Accademia del Cimento held its first session; the year Borelli left, the Cimento quietly died. Indeed, Borelli seems to have been the principal animus of the academy … the Tuscan court had been thoroughly infected by Galileo’s ideas and those of his pupils. Grand Duke Ferdinand II, from the time of his accession to power in 1628 until his death in 1670, maintained a personal laboratory as did Prince Leopold. From the time of the death of the Master, Galileo, informal gatherings met at the court and presented and discussed experiments … Then, possibly under the crystallizing influence of Borelli, Leopold asked for and received permission from Ferdinand to organize formally an academy for purely experimental research. Under Leopold’s aegis it met for the first time in June of 1657 … Lorenzo Magalotti, after attending the University of Pisa as a student, was appointed secretary in 1660. The Cimento had adopted a policy of submerging the identities of its members and presenting itself as a group. Accordingly, when Magalotti brought out the Saggi di naturali esperienzi fatte nell’Accademia del Cimento in 1666–1667, it appeared anonymously and refrained from identifying the individual contributions of the members … During the life of the Cimento dissension appeared among the membership; Borelli may have originated some of it. He seems to have chafed under the requirement of anonymity, and by all accounts he was a touchy person to get along with under any circumstances …
“[Borelli] produced two major studies which were not only exercises in pure mechanics but also, in the eyes of Borelli himself, necessary introductions to what he would consider to be his most important work, the De motu animalium. Respectively, these were De vi percussionis (1667) and De motionibus naturalibus a gravitate pendentibus (1670). Both cover considerably more subject matter than their titles indicate. In the first, for instance, Borelli discusses percussion in detail, some general problems of motion, gravity, magnetism, the motion of fluids, the vibrations of bodies, and pendular motion, to cite just a few items. Likewise, in the second, he argues against positive levity, discusses the Torricellian experiment, takes up siphons, pumps, and the nature of fluidity, tries to understand the expansion of water while freezing, and deals with fermentation and other chemical processes. When we consider that all this was the product of years of experimental and theoretical investigation, we should not wonder that he objected to giving it over to be brought out anonymously by the Cimento just because he happened to present a good deal of it before that society. To the apparent displeasure of Leopold, Borelli published De vi percussionis in Bologna. And in the early summer of 1667 he set out once more to Messina … at this point the Cimento effectively ceased to function, even though it apparently was not formally dissolved, and even though Prince, now Cardinal, Leopold continued to direct some experimental work until he died in 1675. As far as Borelli was concerned, he had been, and afterward remained, on excellent terms with Leopold; and Leopold maintained his high regard for Borelli” (DSB).
Carli & Favaro 303; Cinti 147; De Caro 52; Honeyman 396; Poggendorff I, 240; Riccardi I, 159; Roberts & Trent, Bibliotheca Mechanica, pp. 39-40; Sotheran 474’ Wellcome II, 204. L. Boschiero, Introduction to Borelli’s On the Movement of Animals – On the Force of Percussion, P. Maquet (tr.), 2015; A. Koyré, ‘A Documentary History of the Problem of Fall from Kepler to Newton,’ Transactions of the American Philosophical Society 45 (1955), 329-395.
4to (218 x 162 mm), pp. [xii], 300, 30, [2, errata], with 5 folding engraved plates, printer’s device on title, one ornamental initial. Contemporary Italian speckled calf with double fillet gilt borders to sides; spine richly gilt-tooled in a floral pattern of oriental design, an exquisite and unusual binding clearly intended for presentation.
Item #3935
Price: $15,000.00