Mémoires Mathématiques, Contenant ce en quoy s’est exercé le très-illustre, très-excellent Prince et Seigneur Maurice Prince d’Orange, Conte de Nassau … translate en François par Jean Tuning.
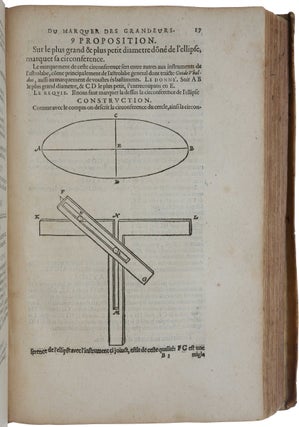
Leyden: Jan Paedts Jacobsz, 1608-05-05-08. Very rare first edition in French of this collection of works, which was published almost simultaneously in Dutch, French and Latin. They deal, among other topics, with geometry, trigonometry, perspective, and double-entry book-keeping – Stevin was one of the first authors to compose a treatise on governmental accounting. The Appendice Algébraique, which Sarton called ‘one of Stevin’s most important publications,’ is the first published general method of solving algebraic equations; it uses what is now called the ‘intermediate value theorem,’ a remarkable anticipation, as it was not rigorously formulated by mathematicians until the nineteenth century. All the works appearing in this volume were first published in this collection (with one exception, where the version here is the earliest extant – see below). Stevin (1548-1620) was perhaps the most original scientist of the second half of the 16th century (the major works of Galileo did not appear until the 17th century). “He was involved in geometry, algebra, arithmetic (pioneering a system of decimals), dynamics and statics, almost all branches of engineering and the theory of music” (Kemp, p. 113). “Stevin unconditionally supported [the Copernican system], several years before Galileo and at a time when few other scientists could bring themselves to do likewise” (DSB XIII: 48). In 1593 Prince Maurice of Nassau (1567-1625) appointed Stevin quartermaster-general of the Dutch armies, a post he held until his death. From 1600 Stevin organized the mathematical teaching at the engineering school attached to Leiden University. “The Prince used to carry manuscripts of [Stevin’s lectures] with him in his campaigns. Fearing that he might lose them, he finally decided to have them published, not only in the original Dutch text [Wisconstighe Gedachtenissen] … but also in a Latin translation by Willebrord Snel [Hypomnemata mathematica] … and in a French translation by Jean Tuning [offered here]” (Sarton, p. 245). The Dutch and Latin editions were published in five parts, of which the fourth consisted principally of reprints of his works on statics that had appeared separately in 1586. This fourth part was not translated into French because, we are told at the beginning of the fifth part, of the printer’s impatience – he was tired of keeping the sheets already printed and suggested that additional materials could be published later when the author had prepared them. The printer’s impatience also accounts for the fact that several works that are announced on the title pages of the individual volumes did not in fact appear in the Dutch, French or Latin editions. The only other complete copy of this French edition listed by ABPC/RBH is the De Vitry copy, in a nineteenth-century binding (Sotheby’s, April 11, 2002, lot 779, £15,200 = $21,935). OCLC lists Columbia, Harvard and UCLA only in US. Provenance: L. Cundier, early inscription on title-pages, i.e., Louis Cundier (c. 1615- 1681), French geometer, surveyor and engraver. He was professor of mathematics at Aix, and was responsible for a Carte géographique de Provence, published about 1640. Contemporary marginal annotation on R6v of final part. The first part of the work, entitled Cosmographie (1608), is a treatise on the trigonometrical techniques used in the observation of the heavens, together with extensive tables of sines, tangents and secants. “The first to use the term trigonometry seems to have been Pitiscus, whose book Trigonometria made its first appearance in 1595, but in 1608, when Stevin’s book appeared, the term had not yet been generally accepted. The book consists of four parts, the first dealing with the construction of goniometrical tables, the second with plane triangles, and the remaining two parts with spherical trigonometry … It is mainly of interest to those who wish to see what trigonometry was like in the sixteenth century, long before Euler, in 1748, introduced the present notation. It also has some distinction as the first complete text on trigonometry written in Dutch; and one of the first – if not the first – written in any vernacular” (Works, IIb, p. 751). Part II, De la Practique de Géométrie (1605) [in Dutch, De Meetdaet], “is primarily a textbook for the instruction of those who, like Prince Maurice, wanted to learn some of the more practical aspects of geometry. The course was not one for beginners, knowledge of Euclid’s Elements being a prerequisite, while the reader was also supposed to know something about the measurement of angles and Stevin’s own calculus of decimal fractions … Parts of the contents were taken from the Problemata Geometrica, the book which Stevin published in 1583, but to which he, curiously enough, never refers. Other parts show the influence of Archimedes and of contemporary writers such as Del Monte and Van Ceulen. Although in accordance with the title strong emphasis is laid on the practical applications of geometry, many theoretical problems are discussed. For Stevin theory and application always went hand in hand. “The Meetdaet appeared in 1605, but it was drafted more than twenty years before. Already in the Problemata Geometrica Stevin refers to a text on geometry, ‘which we hope shortly to publish’ and in which the subject was to be treated by a method parallel to that used in arithmetic. At that time Stevin’s L'Arithmétique was either finished or well advanced. We get the impression that in this period, 1583-85, Stevin decided to publish his full text on arithmetic, but of his text on geometry only those parts which he considered novel. The general outline of the two texts was laid out at the same time, and in close parallel. When at last the Meetdaet appeared, it had undergone many changes, resulting partly or wholly from lengthy discussions with the Prince of Orange. The underlying idea, however, remained the same. “In the introduction to the Meetdaet Stevin explains what he means by this parallelism of arithmetic and geometry. In arithmetic we begin by introducing the numerical symbols, and follow this up by naming them and interpreting their value. Then come the four species, the theory of proportions, the theory of proportional division, and finally the reduction of fractions to a common denominator. Similarly, in geometry, we begin by showing the student how to draw figures, then we name them and explain how to measure them. Then follow the four species, the theory of proportions, of proportional intersections, and the reduction of figures into others of given form and equal length, area or volume. Since these topics are taken in six groups, and each group with lines, plane figures, and solids, the Meetdaet consists of six books, each consisting of three parts. “The opinion of Stevin that geometry and arithmetic have to run parallel is not so artificial as it appears at first sight. Stevin expresses an opinion common to the mathematicians of his age, who insisted on enlarging the field of numbers with irrationals to something like an arithmetic continuum, who applied these numbers without discrimination to the measurement of figures, and for whom numbers were not so much the object of abstract speculation as the tools for surveying, navigation, and astronomy. The subject matter of geometry is continuous quantity, wrote such men as Tartaglia and Clavius. It seemed natural that there should exist relations and analogies between the professed geometrical and the intuitively felt arithmetical continuum. Stevin only gave an early sixteenth-century version of a point of view which was to lead, within the next generations, to analytic geometry. Consciousness of the analogy between arithmetical-algebraic and geometrical considerations continued to work as a leaven throughout the further development of mathematics. Later we find it in Leibniz’ proposal for an algebra of directed quantities. In another form it appeared again more recently when Hilbert probed the consistency of geometrical axioms by means of a corresponding algebraic counterpart. “Book I of the Meetdaet, in accordance with the author’s program, teaches methods for drawing lines and certain plane figures, and for constructing certain solids. With his keen sense of the interdependence of theory and practice Stevin gives not only rules for the drawing board, but also for the surveyor and instrument-maker. We thus meet here with a description of the surveyor’s cross or diopter, already described by Heron and used for setting out perpendiculars by lines of sight. With a graduated circle instead of a cross it becomes a so-called circumferentor or theodolite. The plane figures discussed are the circle, the conic sections, and the Archimedean spiral. No fewer than four methods are given for constructing points of an ellipse when the principal axes are given in position and magnitude … The fourth ellipse construction is equivalent to the one we often use at present, and by which we find points of the ellipse by considering it the oblique parallel or orthographic projection of a circle with one of the axes as diameter. This construction may in this form be original with Stevin, though it is closely related to another one, also presented by Stevin, in which he shows how the conic sections can be constructed as plane intersections of a right circular cone. His method amounts to what we now call orthographic projection … Book I also contains Stevin’s description of the five regular and of eight Archimedean solids … “In Book II we find observations on the lengths of line segments and curves, the areas of two-dimensional figures, and the volumes of solids. Some surveyor’s instruments appear, among them the ancient ‘traprondt’ or graduated circle for measuring horizontal angles, and the equally ancient triquetrum, consisting of two arms of equal length, hinged to a third; they are graduated and have sighting devices. The triquetrum, also called PtoIemy’s rods or parallactic instrument, is used by Stevin to determine a triangle similar to a triangle in the fields, though in his days it had also received attention as a favourite measuring instrument of Copernicus and Tycho Brahe. As an application of the triquetrum Stevin shows us how to measure the distance from a given point to a point beyond reach. A number of other exercises in surveying follow, and also such problems as the computation of the altitudes of a triangle with given sides. In the section on the measuring of circumferences and areas we find a discussion of the value of π with due references to Archimedes, Romanus, and Van Ceulen … “Book III contains the application of four species to geometry, with reference to the parallel treatment in L’Aritbmétique. Multiplication and division of segments, areas, and volumes is only performed by means of numerical factors; there is no reference to the multiplication of segments so as to form areas. Of interest is the addition and subtraction of solids, but the only case discussed is that of similar figures … “In Book IV we find a theory of proportions. It is shown how areas and volumes proportional to given line segments can be found. The most interesting part is that in which the two mean proportionals between two line segments are discussed. As in the Problemata Geometrica, reference is made to Hero’s construction according to Eutocius. The Eratosthenes construction is mentioned, but not further discussed. “Book V contains the division of plane polygons into parts of given ratio by a line satisfying certain conditions, another of the topics of the Problemata Geometrica. Here Stevin goes a little beyond the text of 1583 … he not only modified some of the proofs of the theorems already discussed in the Problemata, but added the cases where the line of division has to pass through a point outside or inside the polygon … “Finally, Book VI deals with some transformations of figures into others of given form and given length, area or volume, such as the (approximate) construction of a straight line equal to the circumference of a given circle, of a triangle equal in area to a given circle, of a sphere equal in volume to a given cone, of a cylinder equal in volume to a given sphere, and of a segment of a sphere, similar to one of two given segments and equal in area to the other” (ibid., pp. 764-8). Part III, Des Perspectives (1605) [in Dutch, Deursichtighe], is a mathematical treatment of perspective. “Stevin’s book gives an important discussion of the case in which the plane of the drawing is not perpendicular to the plane of the ground and, for special cases, solves the inverse problem of perspective” (DSB XIII: 48). “[Stevin’s] approach to perspective belongs in the Commandino – Benedetti – Guidobaldo tradition, and his main demonstrations are uncompromisingly geometrical in nature. He also took up the essentially non-pictorial problem of the rotation of the picture plane into the ground plane, formulating one of the basic theorems of homology. However, he does show some of Marolois’s sensitivity to the needs of practitioners. His treatise was occasioned by the desire of Prince Maurice to understand the principles of pictorial representation – ‘wishing to design exactly the perspective of any given figure with knowledge of causes and mathematical proof’. Stevin accordingly provides ‘abridgements’ of his geometrical techniques for artists – albeit rather abstract abridgements – and illustrates a Dürer-like perspective machine” (Kemp, pp. 113-114). Stevin “was obliged to perform a considerable amount of original work, since most of the books at his disposal had written by and for painters and architects, and were rich in directives and deficient in mathematical demonstrations. The only textbook comparable to that of Stevin in mathematical clarity and antedating it was the Perspectiva of his contemporary and colleague Guido Ubaldo Del Monte (1545-1607), which was published in 1600, only five years before the Deursichtighe. “Stevin’s work contains two books. The title of the first book, Verschaeuwing, is Stevin’s translation of the Latin word scenographia. The term Deursichtighe is his translation of the word perspectiva. Since the second book of the Deursichtighe contains the principles of Spiegelschaeuwen (theory of reflection in mirrors, translation of catoptrica), perspective in Stevin’s terminology comprises both scenography and catoptrics. It also includes the principles of refraction, called Wanschaeflwing, but this subject is wanting in the book” (Works, IIb, p. 785) “There is much in Stevin’s book which reminds us of Del Monte’s, notably the extensive use of rotations and the introduction of the inverse problem of perspective, and the double solution of certain problems, called here the ‘mathematical’ and the ‘mechanical’ way. The two men had much in common; both were experts on fortifications, both were mathematicians deeply interested in problems of mechanics, both combined a love of theoretical study with engineering practice. It is understandable that their approach to perspective was similar, and it is not unlikely that Stevin thoroughly enjoyed Del Monte’s work. Despite this influence (which has to be inferred rather than proved by quotations) Stevin’s work is an achievement of remarkable originality. He probably had a good deal of the contents of his work ready before he studied Del Monte’s Perspective (if ever he did), and maintained his particular way of exposition and selection throughout the book … “The Verschaeuwing itself opens with certain postulates, showing how seriously the author tried to base his work on a correct mathematical foundation. One of these postulates is that a point and its perspective image lie in a straight line with the eye. Stevin’s explanation of the necessity of this postulate is that the physical eye is not a mathematical point; by pressing the eye we can obtain a difference of as much as 33° in the image of a given point. “Among the first constructions are the classical ones of finding the perspective images of a point and a line. Here we meet the demonstration of Del Monte’s theorem that all sets of parallel lines have images in lines passing through one point. This point, ‘saempunt’, is Del Monte’s ‘punctum concursus’. Then comes Stevin’s new approach: he takes the picture plane (the ‘glass’) no longer perpendicular to the ground plane (the ‘floor’), but at an arbitrary angle. This leads him to two new theorems (Props. 7 and 8), by means of which the construction for this case is reduced to the case of the vertical picture plane … Stevin now undertakes the construction of the perspective images of several figures, including that of a ‘tower’, a quadrangular pyramid on top of a cube with a face of the cube as its base; the cube is standing on the ground plane. He also constructs the ellipse as the image of a circle. Some methods of checking the correctness of constructions follow. “These propositions can be considered as forming the first part of the Verschaeuwing. The second part (from Prop. 12 onwards) deals with the inverse problem of perspective, a subject already touched by Del Monte. Given a polygon as image, and another polygon in the ground plane turned into the picture plane: to find, if possible, the eye; the angle between picture plane and ground plane is given and is not necessarily 90°. Stevin solves the problem in certain special cases; the solution of the solution of the general problem had to wait until the nineteenth century. “The text ends with an ‘Appendix’, which contains certain observations on terminology, a correction of certain constructions by Serlio, and a description of a model described by Dürer, which caught the fancy of Prince Maurice to such an extent that he had it constructed. It was an instrument for drawing the perspective of a figure on a glass plate; it had helped Stevin himself to gain a better understanding of the theory. “Book II of the Deursichtighe, the Catoptrics, is short and does not contain much that is of interest … Stevin must have added the sixteen pages as a tribute to an ancient tradition, but he did not develop the subject with his usual thoroughness. That part of the Catoptrics which deals with refraction and which was announced in the Summary, Van de Wanschaeuwing, was not even published” (ibid., pp. 790-1) Part V, Meslanges (1608), contains a very important mathematical work, Appendice algébrique contenant règle générale de toutes Equations, as well as Stevin’s treatise on double-entry bookkeeping. Sections on music, architecture, fortification and other topics, announced on the title page, were never published (in the Dutch, French or Latin editions). The Appendice had been published separately in 1594, but the unique copy, kept at the University of Louvain, was destroyed during World War I and its appearance here is now the earliest extant. “This is one of Stevin’s most important publications: it includes a general rule to solve numerical equations of every degree. Expressed in modern language: if f(a) > 0 and f(b) < 0, there is between a and b at least one root of the equation f(x) = 0” (Sarton, p. 253). This is the first clear statement of what is now known as the ‘intermediate value theorem’, which was rigorously formulated and proved only two centuries later by Bolzano and Cauchy. Stevin tells us that his friend Ludolph van Ceulen had also found a general rule for the same purpose, and it was probably also known to Adrianus Romanus, but priority definitely belongs to Stevin as he was the only one to publish it. “In his Appendice Algébraique Stevin states that after the publication of L'Arithmétique he has found a general rule to solve all equations either perfectly or with any degree of approximation. His example is x3 = 300x + 33915024. To find a first approximation for x, try x = 1, then x = 10, 100, 1000, … The result is that for x = 1, x = 10, x = 100, the value of x3 is less than that of 300x + 33915024, but for x = 1000 it is larger. Hence the first result is 100 < x < 1000. To find a second approximation for x he now substitutes x = 100, 200, 300, 400 and finds 300 < x < 400. Now he tries x = 310, 320, 330 and finds 320 < x < 330, then x = 321, 322, 323, 324. It appears that for x = 324 both sides of the equation are equal, so x = 324 is the root. “The method can also be applied if the root is not an integral number. If x3 = 300x + 33900000 we find 323 < x < 324. Then write x = 3230/10 and proceed as above, first with 1/10, then 1/100, etc. This can go on indefinitely. If, for instance, the root were x = 5/6, the method gives first 8/10, then 83/100, then 833/1000, then 8333/10000, and so we can approach the root as closely as we like. The same holds if x were a radical, incommensurable with common numbers” (Works, IIb, p. 740). The treatise on double entry bookkeeping, Livre de compte de prince à la manière d’Italie, en domaine et finance extraordinaire …, “was composed by Stevin at the request of Prince Maurice, and aptly dedicated to Sully, the great French economist and minister to Henry IV. It is divided into two parts: The merchant’s account book, and the prince’s account book, and the latter part is divided into three others: Livre de compte en domaine, Livre de compte en dépenses, Livre de compte en finances extraordinaires … “The origin of his treatise is clearly explained in the dedication to Sully and in two preliminary dialogues. He recalls his experience as a bookkeeper and cashier in an Antwerp firm and his work in the financial administration of his native city. While doing this work he was struck by the fact that the domanial and financial accounts were kept so badly that princes were always at the mercy of their intendents and receivers, who could deceive them with impunity. It was very soon clear to him that the only way to put a stop to these abuses was to introduce into the public or princely administration the very methods used by merchants. But he had no chance to set forth his views to a competent person until the day came when Maurice of Nassau asked for his advice in that very matter. Stevin explained his ideas of reform to him, and composed the first part of his work; Maurice then asked him to compose the second part (i.e., the prince’s account book). The Prince understood at once the advantage of Stevin’s method and introduced it in his own domains” (Sarton, pp. 263-6). This treatise was issued separately in 1608 in French, and perhaps also in Dutch. “The French translator, Jean Tuning, was secretary to Prince Frederik Hendrik of Nassau (1584-1647), Maurice’s young brother; he was born in Leiden and matriculated at the University of Leiden in 1593” (Sarton, p. 256). Bibliotheca Belgica S.142 (incomplete); Bierens de Haan 4571 (describing only three of the four books); Crone et al (eds.), The Principal Works of Simon Stevin, five vols. (in six), 1955-66; DSB XIII 47-51; Kemp, The Science of Art, 1990, Sarton, ‘Simon Stevin of Bruges (1548-1620)’, Isis 21 (1934), pp. 241-303.
Four parts in one volume (numbered I, II, III & V), folio (310 x 197mm), pp. [12, last leaf blank], 1-234, 231-360; 132; 91; 10, [2, blank], 21, [3], 6, 58, [2], 8, 108 (including ‘Annotation de l’autheur’ on pp. 107-108), [2, blank]. Woodcut device of Stevin on title-page, woodcut device of the printer on other titles, woodcut initials and tailpieces, woodcut diagrams (those on B6r and C2r in part III with pasted-on folding flaps). Contemporary vellum over boards with yapped edges, manuscript title along spine. A fine, unrestored copy but for some intermittent browning which commonly affects this book.
Item #4588
Price: $55,000.00