Problematum geometricorum … libri V.
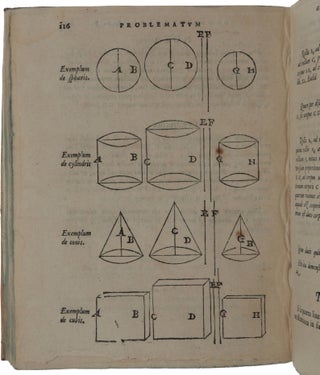
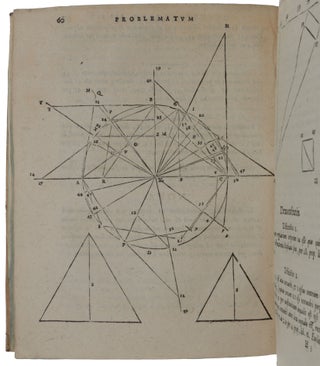
Antwerp: Jean Bellère, [1583]. First edition, very rare, of the principal geometrical work by Stevin, “perhaps the most original man of science of the second half of the sixteenth century” (Sarton, p. 242); this highly original work is his only publication in Latin, and his second-published work (after the Tables of Interest). “He was involved in geometry, algebra, arithmetic (pioneering a system of decimals), dynamics and statics, almost all branches of engineering and the theory of music” (Kemp, p. 113). “Stevin unconditionally supported [the Copernican system], several years before Galileo and at a time when few other scientists could bring themselves to do likewise” (DSB XIII: 48). “Not the least important part of Stevin’s geometrical work is formed by his study of the convex semi-regular polyhedral of the first species, i.e., convex polyhedra whose faces are regular polygons, not all equal and similar to each other, while the solid angles at the vertices are equal and similar to each other without being regular … Besides the regular polyhedra and the semi-regular polyhedra of the first species, in the Problemata geometrica Stevin deals with the five so-called augmented polyhedra, which are produced if on each of the faces of a regular polyhedron as base is erected a regular pyramid whose slant edges are equal to the edges of the base” (Dijksterhuis, pp. 43-45). “Stevin was among the first Renaissance men to study Archimedes with a certain amount of independence. In the Problemata he took some problems he had found in Archimedes' On the Sphere and Cylinder and generalized them somewhat; this gave him an opportunity to apply the methods given by Eutocius for the construction of the two mean proportionals between two lines: a : x = x : y = y : b, a problem which cannot be solved by means of compass and straightedge alone” (Works IIa, pp. 6-7). The work is divided into five books: “Book I. Division of polygons (a) by a line passing through a point of the perimeter or (b) by a parallel to one of the sides. Book II. Application of the regula falsi to mensurations. Book III. Regular polyhedra and semi-regular polyhedra which can be inscribed in a sphere. Book IV. Construction of a solid similar to another, and equal in volume to a third. Book V. Construction of a solid similar to two others and equal in volume to their sum or difference” (Sarton, pp. 248-249). ABPC/RBH list only two copies since Honeyman, both in modern bindings. “Stevin’s contributions to geometry illustrate the fundamental position of Euclid’s Elements in the work of sixteenth-century mathematicians. The Elements were their main source of reference, to which they constantly returned for knowledge, method, and inspiration. The typically ‘Greek’ reasoning of Euclid, which was also basic to the demonstrations of Apollonius and Archimedes, geometrical to the core, was an essential element in the mathematical thinking of sixteenth-century Europe. “This Greek influence was gradually undermined by the adaptation of the arithmetical-algebraic methods traditional in the Orient, which reached Europe almost entirely through authors originally writing in the Arabic language. Stevin’s Tables of Interest present a good example of how the practice of life itself compelled mathematicians to become proficient in these methods. On a higher theoretical level we see the same influence at work in Stevin’s Arithmétique. Even the Problemata Geometrica, though fundamentally a series of papers based on the ‘Greek’ approach, shows the influence of the Arabic tradition in several places. “Several printed editions of the Elements existed in Stevin’s days. One of Stevin’s favourites was the Latin edition by Clavius, the Jesuit astronomer at the Vatican. It was a thorough piece of work, first published in 1574, consisting of two volumes in a rather handy quarto size. It had the advantage of introducing the reader to related work by other mathematicians, explained in Scholia to the text. Other books used by Stevin in preparing his Problemata were Dürer’s Underweysung of 1525 and Commandinus’ Latin edition of the principal works of Archimedes of 1558. “The Problemata consists of five books, each with a topic of its own. The first book, after an introduction on proportions of lines, solves problems concerning the division of polygons into parts of a given ratio. The second book contains the application of the so-called regula falsi to certain constructions or, in other words, shows how certain constructions can be performed with the aid of similarity of figures. In the third book we find Stevin's studies on regular and semi-regular polyhedra. The fourth book deals with the construction of a polyhedron of a given volume similar to a given polyhedron, the fifth book with the construction of a polyhedron similar to two (similar) polyhedra and equal to either their sum or their difference. While the first and second books are based on Euclid, the third is based on Dürer; the last two are the result of Stevin’s study of Archimedes. “The first book opens with a classification of ratios and proportions, based on the fifth book of Euclid’s Elements. This classification, in its attempt to give special names to particular proportions, strikes us as clumsy and pedantic, but Stevin merely followed an ancient tradition. All this labelling was fundamentally due to a serious desire to understand Euclid, though it was encumbered with relics from the works of medieval Latinists … “The next part consists of the application of this theory of proportions to the problem of the division of figures into parts of a given ratio. Stevin found an example of this problem in an appendix by Clavius to the 6th book of the Elements, where it is shown how to divide a triangle into two parts in a given ratio by a line passing through a point on a side. This was not, however, an original idea of Clavius. As he sets forth himself in the Prolegomena to his translation, he found the problem in a book published by Commandinus and John Dee in 1570, which, he says, though ascribed to a certain Mahomed of Bagdad, may have been Euclid’s book on Divisions. Stevin, who did not know this book, took Clavius’ problem and discussed aspects of it in his first set of three problems. Then he himself added five more problems, which he thought to be novel. All eight problems deal with the division of polygons in a given ratio either by a line through a vertex, or by a line through a point on a side, or by a line parallel to a side … Stevin’s work was excellent enough to be preferred by Clavius, who in 1604 praised his treatment of the division of figures above the others … “The second book of the Problemata contains problems involving the so-called ‘regula falsi’, the rule of the false supposition. It is a device to solve problems leading to the linear equation ax = b by first substituting for x an arbitrary number x = x0; if ax0 = b0, then x : x0 = b : b0and x is found by means of proportion … The device also functions for problems which lead to an equation of the form ax + b = c … In the Problemata Stevin introduces this ‘regula falsi’ in accordance with his desire to bring about as close a relation as possible between arithmetical and geometrical proportions. Applying the ‘regula falsi’ to problems in geometry, he has to consider proportions, and this amounts to the solution of certain geometrical problems by means of similarity. If, for instance (Ex. 11), we have to construct a square when the difference between diagonal and side is given, we start with any square (this is the false supposition), determine for this square the difference between diagonal and side, and then find the side of the required square by means of a proportion. All that Stevin now requires is Euclid’s theory of proportions, which he finds in Books V and VI of the Elements. “The third book is by far the most interesting part of the Problemata. It contains a theory not only of the regular solids, but also of certain semi-regular solids and of polyhedra Stevin calls ‘augmented regular solids’. All Stevin had to go by was Euclid's Elements, Book XIII, the so-called XIVth, XVth, and XVIth books, which Clavius also had translated, and Dürer’s Underweysung der Rechnung mit dem Zirckel und Richtscheyt of 1525. From Euclid-Clavius Stevin obtained his information on the five regular solids, from Dürer the method of obtaining semi-regular solids (as well as the regular ones) by paper-folding. To understand these different achievements, we shall denote a polyhedron with m faces which are regular polygons of a sides, n faces which are regular polygons of b sides, etc., by {ma, nb, …}. Then the five regular solids are the tetrahedron {43}, the cube {64}, octahedron {83}, the dodecahedron {125}, and the icosahedron {203}. A semi-regular solid or, as Stevin calls it, a ‘truncated regular solid,’ is defined (Def. 11) as a solid inscribed in a sphere, of which all the solid angles are equal, of which the faces are regular polygons which are not all congruent, and of which all the edges are equal. Dürer had the models of seven such solids: {43, 46}, {83, 68}, {64, 83}, {86, 64}, {184, 83}, {64, 326}, {68, 86, 124}. Dürer had two more models, but one of these, {64, 123}, has some isosceles [i.e. not regular] triangles, while the other, {612, 323}, as Stevin showed, is impossible as a closed polyhedron. “Stevin reconstructed these solids, not only from plane diagrams by folding, but also by finding the method by which these solids are generated by cutting off (truncating) parts of the regular solids. He found three types not described by Dürer … the additional solids {203, 125}, {1210, 203}, and {206, 125}. He was one of the first, if not the first, in Renaissance days to find all these ten … “The third book of the Problemata also contains a description of what Stevin called ‘augmented regular solids’. These are polyhedra obtained by placing on top of each face of a regular polyhedron as base a pyramid with equal edges. Stevin lists all five of them. He was led to the consideration of these solids by a discovery of Frans Cophart, leader of the Collegium Musicum at Leiden. Cophart had taken a cube and cut out twelve tetrahedra, each having the end points of an edge and the midpoints of the faces through this edge as vertices. The solid thus obtained by ‘faceting’ the cube is what is now called the stella octangula; it is bounded by twenty-four congruent equilateral triangles. Cophart had claimed it as a sixth regular solid. “Stevin, while admiring the discovery, had to deny this claim. He pointed out that the vertices of Cophart’s solid do not all lie on one sphere, but are distributed on two spheres, six on one sphere and eight on a concentric one. At the same time he discovered another construction of the solid by starting, not from a cube and then faceting it, but from an octahedron and then ‘augmenting’ it by placing a regular tetrahedron on each face with this face as base. He now saw that this procedure could be applied to all regular bodies, and in this way he obtained four new polyhedra. “Of all these five solids of Stevin we only call the stella octangula a regular star-polyhedron. The reason is that regular star-polyhedra are obtained from the regular polyhedra by the process of ‘stellating,’ i.e., by producing the planes of the faces and allowing non-adjacent faces to intersect in such a way that the faces of the new solid are regular star-polygons (polygons obtained by allowing non-adjacent sides of regular polygons to intersect). This procedure does not yield a new body in the case of the regular tetrahedron and the cube, but gives us the stella octangula in the case of the regular octahedron. We also obtain regular star-polyhedra by stellating the regular dodecahedron and icosahedron; for each of these solids we obtain two possible star-polyhedra. But whereas these four bodies are single, the stella octangula is found to be the intersection of two regular tetrahedra. We may thus speak of nine regular solids: five ordinary (Platonic) and four stellated ones … “The fourth and fifth books of the Problemata Geometrica present Stevin to us as a student of Archimedes. The editio princeps of Archimedes’ works had appeared at Basle in 1544; it contained not only the original Greek text and a Latin translation, but also the precious commentaries of Eutocius, again both in Greek and in Latin. Another useful, though limited, edition was the Latin translation of five of Archimedes’ treatises with Eutocius’ commentary on one of them, prepared by Commandinus and published in 1558. Stevin quotes Commandinus’ edition, but he must also have known the editio princeps, since he shows himself to be acquainted with material which is to be found in the publication of 1544, but not in that of 1558. “Archimedes, in the book On the Sphere and Cylinder, the book in which he determines the area and the volume of the sphere, solves some problems which involve the finding of the two mean proportionals between two given lines. An example is formed by the problem: ‘given two spherical segments, to find a third segment similar to the one and having its volume equal to that of the other’; another example consists in the problem of finding a sphere equal in volume to a given cone or cylinder … Moreover, in Commandinus’ edition, though it does not contain the book On the Sphere and Cylinder with its commentaries, there are several problems which belong to the same group. The first is the problem: ‘Given any two cones (or cylinders), to find a third cone (or cylinder), equal in volume to the first and similar to the second’ … “Stevin, in his fourth book, casts the problem into its general form: ‘Given two solids S1, S2, to find a third solid equal to S1 and similar to S2 … Stevin uses the general term ‘solid’ then makes use of the theorem that any solid can be changed into a cone of equal volume; he actually applies the theorem to … polyhedra, circular cones, cylinders, and to segments of cones. Stevin shows, for instance, how a spherical segment can be changed into a cone with equal base … “Stevin’s procedure is as follows: a) he changes S1 into a circular cone C1 and S2 into a circular cone C2; b) he then changes C1 into a cone C1' of the same altitude as C2; c) he then constructs a cone C3, similar to C2 and equal to C1'; d) he then changes C3 into an equal solid S, reversing the process by which S was changed into C2. The steps a), b), d) only involve ordinary proportions, step c) involves the construction of two mean proportionals; for this purpose Stevin mentions Hero’s construction, on which Eutocius reports. “… in the last book of the Problemata, [Stevin] solved another problem leading to two mean proportionals between two lines, which appears to be a new one. Given two similar solids S1 and S2,S1 > S2, Stevin asked to find a solid similar to S1 and S2, and equal to a) the sum of, b) the difference between S1 and S2. The problem was again solved by reducing the solids to circular cones” (Works IIa, pp. 121-130). The Problematum geometricorum was not included in Stevin’s collected works (Hypomnemata mathematica, 1605), of which the second volume was devoted to geometry. “This work is different from the Problemata geometrica and inferior to it; it is also a collection of geometrical problems but it is not arranged as logically as the former; it was chiefly made to complete the Prince’s geometrical training” (Sarton, p. 261). Adams S1858. Crone et al. (eds.), The Principal Works of Simon Stevin, five vols. (in six), 1955-66; Dijksterhuis, Simon Stevin, Science in the Netherlands around 1600, 1970; Kemp, The Science of Art, 1990; Sarton, ‘Simon Stevin of Bruges (1548-1620)’, Isis 21 (1934), pp. 241-303.
4to (200 x 157 mm), pp. [4], 5-118, [1], with woodcut printer’s device on title, numerous woodcut diagrams in text, and errata on recto of last leaf. Contemporary limp vellum with remains of ties (hole in upper part of spine, probably due to insect damage, f. I2 with several tiny tears in gutter without loss). A very good unrestored copy.
Item #4928
Price: $25,000.00