VIÈTE, François (SCHOOTEN, Frans van, ed.).

Opera Mathematica in unum volumen congesta...

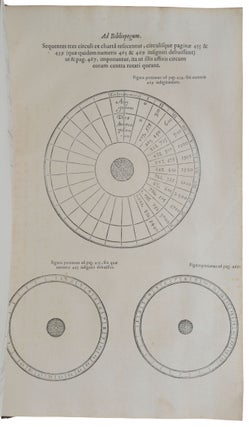
Leiden: Bonaventure & Abraham Elzevier, 1646.

First collected edition, rare, of the mathematical writings of François Viète (1540-1603), the greatest French mathematician of the sixteenth century, who was “the first extensively to use letters of the alphabet to represent numerical quantities” (Hutchinson’s Dictionary of Scientific Bibliography, p. 690), and “the first mathematician of his age to think occasionally as mathematicians habitually think today” (Bell, p. 99). Viète used letters “both for known … and for unknown quantities” and “this innovation, considered one of the most significant advances in the history of mathematics, prepared the way for the development of algebra” (DSB); it earned him the sobriquet “the father of algebra” (ibid.). Viète’s Isagoge in artem analyticam, the earliest work on symbolic algebra, opens the present edition and is followed by 15 further tracts on algebra, numerical analysis, geometry, trigonometry, and the newly adopted Gregorian calendar, the last of which include three volvelles (here bound in uncut on a separate sheet). Viète developed “the systematic application of syncopated algebra to the solution of geometric problems” and thus is widely considered to have paved the way for René Descartes’s invention of analytic geometry. The young Isaac Newton carefully worked through a copy of the Opera when he was studying in Cambridge (Whiteside, p. 21), and this influenced his own work on algebra and analytic geometry. The Opera was edited by the influential Leiden University mathematician Frans van Schooten (1615-60), who numbered among his students the young Christiaan Huygens. Schooten later (1659-61) published an important edition of Descartes’s Géométrie with explanatory notes, along with several treatises of his own and his students. The idea of printing an edition of Viète’s works was suggested to the Elzevirs by Marin Mersenne in 1638, and the proposed work was advertised in 1640 (in the first number of the Catalogus Universalis), but it did not appear until six years later because of the difficulties which Schooten experienced in finding copies of the individual works, which were already rare less than fifty years after their publication. All of them are virtually unobtainable today in their original printings, and the present volume is therefore the closest a modern collector can hope to approach the original writings of Viète. The Opera includes all of Viète’s published writings, with the exception of the Canon triangulorum (1579) – Schooten misinterpreted a remark of Viète’s which seemed to imply that the tables were inaccurate and so chose to omit the work – and the semi-popular Principes de Cosmographie (1637). Viète’s principal astronomical treatise, the Harmonicum coeleste, which inspired many of his other works, remains unpublished today.

“Viète’s initial goal in his mathematical work was the development and improvement of geometric models for calculations in planetary astronomy. Delambre gave the right perspective when he wrote in his 1819 Histoire de l’Astronomie du Moyen Age that Viète ‘was not an astronomer, but he was the greatest geometer of his time’. Like Ptolemy, Viète considered geometry to provide the theoretical foundation for astronomical calculations, and through his trigonometric investigations he found a way to create an algebra for geometry that surpasses traditional numerical algebra in its flexibility, generality, and utility. In the process of creating this new algebra, Viète gave algebra a grounding in Euclid’s Elements and he renovated geometric analysis through the algebrization of the transformational rules of Euclidean geometry” (Oaks, pp. 296-7).

Schooten organised Viète‘s treatises by topic: the first four are algebraic, then the one treatise on numerical solution of equations, followed by eight geometrical works, and concluding with three on the calendar. We give the titles of the individual works as they originally appeared, which sometimes differ slightly from their titles in the Opera.

The volume opens with In artem analyticum isagoge (pp. 1-12), first published at Tours in 1591, “a text in which Viète proposed nothing short of a complete refashioning of algebra as it was then understood … Rather than viewing algebra merely as the search for solutions of particular equations, he understood it as the analysis of an actual theory of equations” (Katz & Parshall, pp. 236-237). “The most important of Viète‘s many works on algebra … [It] introduced the use of letters both for known quantities, which were denoted by the consonants B, C, D, and so on, and for unknown quantities, which were denoted by the vowels. Furthermore, in using A to denote the unknown quantity x, Viète sometimes employed A quadratus, A cubus ... to represent x², x³, ... This innovation, considered one of the most significant advances in the history of mathematics, prepared the way for the development of algebra” (DSB). “If this seems reminiscent in principle of our modern notation of x, y, and z for unknowns and a, b, c, etc. for indeterminate magnitudes, a convention which we owe to René Descartes in the seventeenth century, it is important to recognize that Viète’s symbols or ‘species’, unlike ours, carried explicit geometrical meaning. They had dimension, and only expressions of the same dimension were commensurate … To Viète’s way of thinking, then, the addition of a one-dimensional unknown A to a one-dimensional indeterminate B was denoted simply by A + B (we would write x + b), but in two dimensions, the sum appeared as A square + B plane (or our x² + b) and in three dimensions as A cube + B solid (or our x³ + b)” (Katz & Parshall, pp. 238-239).

Perhaps the most important part of the work is chapter 4, in which “he presents a mode of calculation carried out completely in terms of ‘species’ of numbers and calls it logistice speciosa – in contrast with calculation using determinate numbers, which is logistice numerosa. Of significance for the formation of the concepts of modern mathematics, Viète devotes the logistice speciosa to pure algebra, understood as the most comprehensive possible analytic art, applicable indifferently to numbers and to geometric magnitudes” (DSB).

Viete’s ‘Analytic Art’ comprises three stages. At the first stage, zetetics, a problem, whether of arithmetic or geometry, is translated into Viète’s newly created symbol system or logistice speciosa in the form of an equation. At the second stage, poristics, equations are transformed according to rules into canonical forms; and finally at the third, exegetics, a solution to the problem is found on the basis of the derived equation. As Viète himself emphasizes, at this third stage the analyst turns either geometer, ‘by executing a true construction,’ or arithmetician, ‘solving numerically whatever powers, whether pure or affected, are exhibited.’ Each of Viète’s treatises (with the exception of those on the calendar) can be seen as instances of his Art.

“To the treatises of the Isagoge belong Ad logisticen speciosam, notae priores (pp. 13-41) and Ad logisticen speciosam, notae posteriores, the latter now lost. The first was not published during his life, because Viète believed that the manuscript was not yet suitable for publication. (It was published by Jean de Beaugrand in 1631.) It represents a collection of elementary general algebraic formulas that correspond to the arithmetical propositions of the second and ninth books of Euclid’s Elements, as well as some interesting propositions that combine algebra with geometry. In propositions 48-51, Viète derives the formulas for sin 2x, cos 2x, sin 3x, cos 3x, sin 4x, cos 4x, sin 5x and cos 5x expressed in terms of sin x and cos x” (ibid.). He notes that the coefficients are equal to those in the binomial expansions of (a + b)², (a + b)³, etc.

“In 1593 Viète published Zeteticorum libri quinque (pp. 42-81), which he very probably had completed in 1591. In it he offered a sample of logistice speciosa and contrasted it directly with Diophantus’ Arithmetica, which, in his opinion, remained too much within the limits of the logistice numerosa … The Zetetics is composed of five books, the first of which contains ten problems that seek to determine quantities of which the sum, difference, or ratio is known. The problems of the second book give the sum or difference of the squares or cubes of the unknown quantities, their product, and the ratio of this product to the sum or the difference of their squares. In the third book the unknown quantities are proportional, and one is required to find them if the sum or the difference of the extremes or means is given. This book contains the application of these problems to right triangles. The fourth book gives the solutions of second-and third-degree indeterminate problems, such as to divide a number, which is the sum of two squares, into two other squares. The fifth book contains problems of the same kind, but generally concerning three numbers” (ibid.).

Although it was composed before 1593, De Æquationum Recognitione et Emendatione Tractatus Duo (pp. 82-161) “was published in 1615, under the editorship of Viète’s Scottish friend Alexander Anderson. The treatise De emendatione contains the subject matter of the work as announced in the Isagoge under the title Ad logisticen speciosam notae posteriores and sets forth a series of formulas (notae) concerning transformations of equations. In particular it presents general methods for solving third- and fourth-degree equations. This work reveals Viète’s partial knowledge of the relations between the coefficients and the roots of an equation. Viète demonstrates that if the coefficient of the second term in a second-degree equation is minus the sum of two numbers the product of which is the third term, then the two numbers are roots of the equation. Viète rejected all but positive roots, however, so it was impossible for him to perceive fully the relations in question” (ibid.).

“In the 1591 edition of the Isagoge, Viète had already given the outline of the De numerosa potestatum purarum, atque adfectarum ad exegesin resolutione tractatus (pp. 162-228). The ‘numerical resolution of powers’ referred to in the title means solving equations that have numerical solutions, such as x² = 2916 or x² + 7x = 60750. The work was published in 1600 at Paris, edited by Marino Ghetaldi, with Viète’s consent … Viète gave some of his manuscripts to Ghetaldi when the latter was in Paris. Ghetaldi took them to Rome and allowed his friends there to make a copy. After Viète’s death his heirs gave other manuscripts to his friend Pierre Alleaume, who left them to his son Jacques, a pupil of Viète’s. Jacques entrusted Anderson with the treatises De aequationum recognitione, Notae ad logisticem posteriores, and Analytica angularium sectionum. In De numerosa potestatum, Viète gives a method of approximation to the roots of numerical equations that resembles the one for ordinary root extraction. Taking f(x) = k, where k is positive, Viète separates the required root from the rest, then substitutes an approximate value for it and shows that another digit of the root can be obtained by division” (ibid.).

The geometrical part of the Opera opens with Effectionum Geometricarum Canonica Recensio (pp. 229-239), first published at Tours in 1593. “‘With a view to exegetic in geometry, the analytical art selects and enumerates more regular procedures by which equations of ‘sides’ and ‘squares’ may be completely interpreted’ – that is, it concerns a convenient method for solving geometrical problems by using the coefficients of the equation in question, without solving the corresponding equation. All the solutions he gives in this tract have been carried out by geometric construction with the ruler and compass: for instance, the proof of proposition X, which leads to the equation x² - px = q², and that of proposition XVII, which leads to the equation x⁴ + p²x² = p²q²” (ibid.).

“In 1593 at Tours, Jamet Mettayer edited Francisci Vietae Supplementum geometriae, ex opere restitutae mathematicae analyseos seu algebra nova (pp. 240-257) … The tract begins with the following postulate: ‘A straight line can be drawn from any point across any two lines (or a circle and a straight line) in such a way that the intercept between these two lines (or the line and the circle) will be equal to a given distance,’ any possible intercept having been predefined. The twenty-five propositions that follow can be divided into four groups: 1. Propositions 1-7 contain the solution of the problem of the mesographicum – to find two mean proportionals between two given straight line segments – and its solution immediately yields the solution of the problem of doubling the cube. 2. Propositions 8-18 contain the solution of the problem of the trisection of an angle and the corresponding cubic equation. The trigonometric solution of the cubic equation occurs twice: in proposition 16 and 17. 3. Proposition 19-24 contain the solution of the problem of finding the side of the regular heptagon that is to be inscribed in a given circle. 4. Proposition 25 explains the importance of the applied method: the construction of two mean proportionals, the trisection of an angle, and all problems that cannot be solved only by means of the ruler and compass but that lead to cubic and biquadratic equations, can be solved with the aid of the ancient neusis procedure [which is embodied in his initial postulate]” (ibid.).

“In 1592 Viète began a lively dispute with J. J. Scaliger when the latter published a purported solution of the quadrature of the circle, the trisection of an angle, and the construction of two mean proportionals between two given line segments by means of the ruler and compass only. In that year Viète gave public lectures at Tours and proved that Scaliger’s assertions were incorrect, without mentioning the name of the author. For this reason he decided in 1593 to publish book VIII of his Variorum de rebus mathematicis responsorum Liber VIII, cuius praecipua capita sunt: De duplicatione cubi et quadratione circuli, quae claudit πρχóειρov seu ad usum mathematici canonis methodica [pp. 347-435]. In chapters 1, 2, and 5 Viète treats the traditional problem of the doubling of the cube, that is, of the construction of two mean proportionals … In chapter 3 he is concerned with the trisection of the angle and, in chapter 7, with the construction of a regular heptagon to be inscribed in a given circle, proposed by François de Foix, count of Candale, the most important contemporary editor and reviser of Euclid. Chapters 6 and 14 are related to Archimedes’ On Spirals, already known in the Latin West through the Moerbeke translation of 1269. In chapter 8 Viète discusses the quadratrix and, in chapter 11, the lunes that can be squared. He investigates the problem of the corniculate angle [the angle between a circle and a straight line tangent to it] in chapter 13 and sides with Peletier, maintaining that the angle of contact is no angle. Viète’s proof is new: the circle may be regarded as a plane figure with an infinite number of sides and angles; but a straight line touching a straight line, however short it may be, will coincide with that straight line and will not form an angle. Never before had the meaning of ‘contact’ been stated so plainly. In chapter 16 Viète gives a very interesting construction of the tangent to the Archimedean spiral and, in chapter 18, the earliest explicit expression for π by an infinite number of operations … The trigonometric portion of this treatise begins with chapter 19 and concerns right and oblique plane and spherical triangles …

“Since Scaliger could not defend himself against Viète’s criticism, he left France for the Netherlands, where soon after his arrival in 1594 he published his Cyclometrica elementa, followed some months later by his Mesolabium. Viète responded with Munimen adversus cyclometrica nova (1594) [pp. 436-446] and Pseudomesolabium (1595) [pp. 258-304]. In the first, through a nice consideration based on the use of the Archimedean spiral, he gives two interesting approximations of a segment of a circle. In the second he seeks those chords cutting the diameter in such a way that the four parts increase in geometric series. In the appendix Viète refutes Scaliger’s assertion that in the inscribed quadrilateral the diameter and both diagonals are in arithmetical proportion.

“Viète’s mathematical reputation was already considerable when the ambassador from the Netherlands remarked to Henry IV that France did not possess any geometricians capable of solving a problem propounded in 1593 by Adrian Romanus to all mathematicians and that required the solution of a forty-fifth-degree equation. The king thereupon summoned Viète and informed him of the challenge. Viète saw that the equation was satisfied by the chord of a circle (of unit radius) that subtends an angle 2π/45 at the center. In a few minutes he gave the king one solution of the problem written in pencil and, the next day, twenty-two more. He did not find forty-five solutions because the remaining ones involve negative sines, which were unintelligible to him. Viète published his answer, Ad problema, quod omnibus mathematicis totius orbis construendum proposuit Adrianus Romanus, responsum [pp. 305-324], in 1595 …

“At the end of his work Viète proposed to Romanus, referring to Apollonius’s Tangencies, the problem to draw a circle that touches three given circles. Romanus was acquainted with Regiomontanus’ statement that he doubted the possibility of a solution by means of the ruler and compass only. He therefore solved the problem by determining the center of the required circle by means of the intersection of two hyperbolas; this solution did not, however, possess the rigor of the ancient geometry. In 1600 Viète presented a solution that had all the rigor desirable in his Apollonius Gallus [pp. 325-346], in which he gave a Euclidean solution using the center of similitude of two circles. Romanus was so impressed that he traveled to Fontenay to meet Viète, beginning an acquaintanceship that soon became warm friendship. Viète himself did not publish the book; very probably it was done by Marino Ghetaldi” (ibid.).

“Viète also had a role in the improvements of the Julian calendar. The yearly determination of the movable feasts had long resulted in great confusion. The rapid progress of astronomy led to the consideration of this subject, and many new calendars were proposed. Pope Gregory XIII convoked a large number of mathematicians, astronomers, and prelates, who decided upon the adoption of the calendar proposed by Clavius. To rectify the errors of the Julian calendar, it was agreed to write 15 October into the new calendar immediately after 4 October 1582” (ibid.). The proposal for the Gregorian calendar was published as Kalendarium Gregorianum perpetuum (1582), and is reprinted in the Opera (pp. 504-533).

“The Gregorian calendar met with great opposition among scientists, including Viète and Tobias Müller. Viète valued the studies involved in a reform of the calendar; and toward the end of his life he allowed himself to be carried away by them and to engage in unjustified polemics against Clavius, the result of which was the publication with Mettayer of Libellorum supplicum in regia magistri relatio kalendarii vere Gregoriani ad eccelesiasticos doctores exhibita pontifici maximo Clementi VIII anno Christo 1600 iubilaeo (1600) [pp. 447-503]. He gave the work to cardinal Cinzio Aldobrandini, who transmitted it to Clavius. Since Clavius rejected the proposed corrections. Viète and Pierre Mettayer, the son of Jean, published a libel against Clavius that was as vehement as it was unjust: Francisci Vietae adversus Christophorum Clavium expostulatio (1602) [pp. 534-544]” (ibid.). The controversy ended only with Viète’s death in 1603.

Remembered principally for his mathematical work, Viète was a lawyer by trade, serving as a privy counsellor to Henry III and Henry IV, for whom he worked primarily as a code-breaker during the French Wars of Religion.

Bierens de Haan 4225; Brunet V, 1212; Norman 2152; Willems 609; Cajori, A History of Mathematics, pp. 137-39; D.S.B., XIV, pp. 18-25; Bell, The Development of Mathematics, 1945; Boyer, History of Analytic Geometry, 1956; Katz & Parshall, Taming the Unknown, 2014; Oaks, ‘François Viète’s revolution in algebra,’ Archive for History of Exact Sciences 72 (2018), pp. 245-302. Whiteside (ed.), The Mathematical Papers of Isaac Newton, vol. 1, 1664-1666, 1967.

Folio (308 x 195 mm) in 4s, pp. [xii], 554, with sheet of uncut volvelles bound between 3L3 and 3L4 (occasional light browning). Eighteenth-century speckled sheep, spine richly gilt in compartments with red morocco lettering-piece (a little rubbed).

Item #4931

Price: $12,500.00