Ausszug auss der uralten Messekunst Archimedis vnd deroselben newlich in Latein aussgangener Ergentzung...
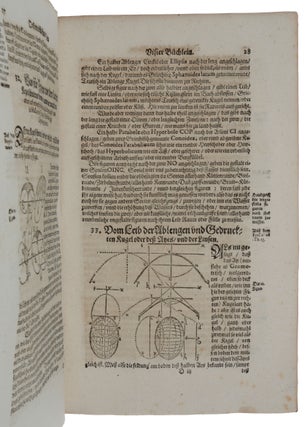
Linz: Hans Blanck, 1616. First edition, a considerably revised, rearranged and augmented version of Kepler’s Nova Stereometria published the year before, a work which is “generally regarded as one of the significant works in the prehistory of the calculus” (Gingerich in DSB). “Desiring to outfit his new household with the produce of a particularly good wine harvest, Kepler installed some casks in his house. When he discovered that the wine merchant measured only the diagonal length of the barrels, ignoring their shape, Kepler set about computing their actual volumes. Abandoning the classical Archimedean procedures, he adopted a less rigorous but productive scheme in which he considered that the figures were composed of an infinite number of thin circular laminae or other cross sections. Captivated by the task, he extended it to other shapes, including the torus” (DSB). The Messekunst is not a simple translation of the Nova stereometria. The material is substantially reorganized, the Theorem-proof structure of the earlier work replaced by a more informal approach (that structure had proved unsuitable for a practical audience and sales of the Nova stereometria were disappointing). Most importantly, the Messekunst contains material not present in Nova stereometria: first, the solution to the difficult problem of finding the volume of wine in a partly empty barrel, which had been mentioned but not solved at the end of the earlier work; second, the explanation of the effectiveness of the ‘gauging rod’ used by Austrian wine merchants to measure the volume of their barrels, which had prompted Kepler’s work on ‘doliometry’ in the first place; and finally, the Anhang (Appendix), on weights and measures from antiquity to Kepler’s time, is present only in the Messekunst, as is the German/Latin glossary “that established the beginnings of German mathematical terminology” (Baron, p. 110). This copy of the Messekunst has the printed gauge slip on K1, not recorded by Caspar; it duplicates the figure printed within the text. The Messekunst is significantly rarer than the Nova stereometria in commerce: RBH lists three other copies of the former at auction in the last half-century, and nine of the latter. Kepler (1571-1630) became interested in stereometry as a result of a serendipitous event that took place in November 1613 in Linz, where Kepler was then living. Kepler purchased some barrels to lay in a supply of wine for his family and had them delivered to his house. When the wine dealer came to the house to measure the volume of wine the barrels contained, he used the standard gauger’s technique which in effect meant approximating the barrel by a cylinder of the same height as the barrel but with cross-sectional area equal to the average of the area of the ends of the barrel and that of its middle bulge. Thus, the approximate formula for the volume of the barrel was V = ½ x height x (end-diameter2 + bulge-diameter2) V0, where V0 was the known volume of a cylinder of unit height and diameter. To simplify the calculation a gauging rod was used. This was a rod marked with a quadratic scale (i.e., 1 at the first mark, 4 at the second, 9 at the third, etc.); by laying it across the end of the barrel, then inserting it through the bung hole in the middle of the bulge, and reading off the numbers on the scale, the gauger could then calculate an approximation to the volume of wine in the barrel by using the above formula. Kepler was more than sceptical about the accuracy of this method of volume determination, especially how it could work for barrels of any shape and size, and he immediately decided to try to find a better mathematical method, and one that would also deal with the case of partly empty barrels, for which the gauger had no solution. By December 17, 1613 Kepler believed that he had reached his goal. He had composed a short six-page manuscript with about ten theorems, and with a dedication to Prince Maximilian of Liechtenstein and Baron Helmhard Jörger as a New Year gift. Around February 1, 1614 Kepler sent the manuscript to Markus Welser in Augsburg to have it printed, there being at that time no printer in Linz. On February 11, Welser replied that he had received the manuscript and had discussed publication with the Augsburg bookseller Hans Krüger. Although he accepted that Kepler’s name was highly respected in academic circles, Krüger felt that the work would sell poorly, especially in Latin. Krüger accepted Welser’s suggestion that the book be printed at Kepler’s expense, but before a printer could be found Welser died on June 23. The manuscript remained with Krüger and may have been forgotten by Kepler had a new printer not arrived in Linz. In the spring of 1615, the printer Hans Blanck or (Planck) arrived in Linz from Erfurt and offered his services. Kepler remembered his manuscript, which was still in Augsburg, and demanded it back. He received it with much effort at the end of May (1615), but immediately realised that it was unsatisfactory. As well as being too brief, there was also a serious mistake in it, and he was forced to rewrite it. The new version of Stereometria grew considerably compared to the original, the Supplementum ad Archimedem was added, as well as the entire second part. But by July 15, after only six weeks, the work was done. The Stereometria doliorum, the first book printed in Linz, was available at the autumn 1615 book fair at Frankfurt. “In this work Kepler uses a wide range of methods including visual imagery, geometric transformation, analogy and tabulation but most of all the cutting of small sections varying in size and shape, parallel to no given direction and chosen at will in the most convenient form to meet the needs of a particular problem. Probably no one since Kepler has used infinitesimals quite so freely” (Baron, p. 110). Kepler’s stereometrical work “exerted such a strong influence in the infinitesimal considerations which followed its appearance, and which culminated a half century later in the work of Newton, that it has been called [by Moritz Cantor] the source of inspiration for all later cubatures" (Boyer, p. 110). It also contains the germ of the differential calculus: Kepler “showed, among other things, that of all right parallelepipeds inscribed in a sphere and having square bases, the cube is the largest, and that of all right circular cylinders having the same diagonal, that one is greatest which has the diameter and altitude in the ratio of √2 : 1. These results were obtained by making up tables in which were listed the volumes for given sets of values of the dimension … He remarked that as the maximum volume was approached, the change in volume for a given change in the dimensions became smaller” (ibid.). Kepler had noted, in modern terms, that when a maximum occurs the rate of change becomes zero, a basic principle of the differential calculus that is usually credited to Fermat later in the century. In the first and longest part of the Nova stereometria Kepler introduces an ingenious ‘unfolding’ technique for calculating areas and volumes, with which he obtains certain results which Archimedes had obtained by a reductio ad absurdam argument (Kepler refers explicitly to Archimedes’ Dimension of the Circle, Quadrature of the Parabola, etc.). The simplest case is that of a circle, which can be divided into an infinitely large number of triangles, each with one vertex at the centre of the circle, the other two vertices being infinitesimally nearby points on the circumference. Unfolding the circumference of the circle onto a straight line gives a series of triangles all with the same height equal to the radius of the circle. Since the area of a trangle equals ½ x base x height, the total area of the unfolded triangles is ½ x circumference x radius, which is the correct formula for the area of a circle. “The properties of circular cylinders, cones and prisms can all be derived by similar considerations. The sphere can be regarded as made up of infinitely many small cones, each with its base on the surface of the sphere and its vertex at the centre … “[In the Supplementum ad Archimedem,] Kepler considers the rotation of certain closed figures about axes in the plane. Whereas Archimedes had confined himself to rotations about the principal axes, Kepler generates a variety of different solids by rotating about lines in the plane other than the principal axes. A solid formed by rotating a plane figure about a line in the plane which does not intersect the curve is called a ring. If the line is parallel to an axis of symmetry the volume of the ring is equal to that of a cylinder with height equal to the circumference of the circle described by the centre of the figure and with base equal to the section itself” (Baron, pp. 110-111). Kepler proved this by cutting the ring into infinitely many thin slices by planes passing through the axis. Similar but more difficult techniques can be used when the axis of rotation does intersect the figure being rotated. As examples, Kepler determined the volume of solids obtained by the rotation of circular segments around chords of the circle, which produced a variety of solids which he named after fruits: rotating a circle about a chord of the circle gave an apple; rotating the minor segment cut off by the chord about the chord gave a lemon; there was also a plum, a spindle, etc. “In all Kepler considers the volumes of 96 different solids obtained by rotating segments of conic sections (ellipses, parabolas, hyperbolas) about various axes” (Baron, p. 115). In Part 2 Kepler explored the solid geometry of the Austrian barrel, approximating the barrel as a cylinder or as two truncated cones joined at their larger base. He studied the dependence of the volume of a barrel with fixed diagonal on the ratio of the stave length to the diameter of the bottom, and of the largest diameter of the belly to that of the bottom. For Austrian barrels, it was the rule among coopers that the radius of the barrelhead should be one-third of the length of the staves, whereas for Rhineland casks the radius of the barrelhead was equal to one-half of the length of the staves. Kepler showed that the volume of the ‘truncated lemon’ (or ‘hyperbolic spindle’), which he was able to calculate, gave the best approximation for the Austrian barrels. In part 3, Kepler showed that the Austrian barrel was the most reliable shape because slight errors in construction would have minimal effect on its volume as measured by the gauging rod. Other shapes were less reliable, a conclusion that must have delighted Kepler’s Austrian patrons. In discussing how to find the volume of a barrel of arbitrary shape Kepler described a tool for recording the cross-sectional shape of a surface, very like the modern ‘contour gauge.’ “Kepler denounces the imprecise use in these [wine] casks of the ‘cubic ruler’ designed to measure their content. He saved the explanation of this ruler – a wooden stick, which, he says, is supplied with each cask without variation or calculation, and regardless of the cask’s shape – for the book he went on to publish a year later, Ausszug auss der uralten Messekunst Archimedis” (Radelet-de Grave, p. 60). The Nova stereometria did not sell well. “Kepler had presented a copy of the Stereometria to the Dantzig mathematician Crüger [i.e., Peter Crüger (1580-1639), who had been a student of Kepler] with the request to advertise his work. Crüger replied (letter dated July 31, 1616) that apart from him only his Königsberg colleague, the Königsberg library and a Prussian noble named Niewieschinsky were buyers. Nevertheless, Kepler apparently got his money’s worth. On June 17, 1616, he wrote back to Crüger: ‘You are giving me to understand that there is no prospect of selling copies. But that does no harm, I had already forgotten about this matter. I wrote for the Austrians; they have already paid and will pay a little more’” (Hammer, our translation). Kepler’s patrons were also unimpressed with the work, and they advised their mathematician to concentrate on the matter specified in his contract: the completion of the Rudolphine Tables. Kepler, however, immediately began to rework the book for those not proficient in Latin or advanced mathematics, recognising that it was results rather than derivations that were important for gaugers. There were probably also financial considerations. “A German edition was prompted in part by having Planck sitting idle and also by the opportunity it presented of widening the circle of presentation copies for which Kepler would receive the customary financial reward. Such honoraria were often more lucrative than the actual sale of the book. In the case of the German edition, Kepler already had the woodblocks for the illustrations, so he only had to pay for new typesetting and printing. Once he had distributed the presentation copies and tallied up the honoraria he received in return, he covered the production costs and raked in at least 40 florins pure profit before selling a single copy … he needed the money for his next big publishing venture, an astronomical textbook [i.e., the Epitome astronomiae Copernicanae]” (Voelkel, pp. 82-83). The preparation of the Messekunst took a relatively long time. It was only after five months, around Christmas 1615, that it was finished; the dedication to the state of Oberösterreich was dated January 1, 1616. Altogether, Kepler wrote in a letter to Mästlin, he spent nine months on stereometry. The Messekunst was in Frankfurt for the spring fair. “The structure of the Messekunst runs parallel to that of the Stereometria. Like the latter, it has three parts: the first (Nos. 4-67) contains the most important theorems from ‘Archimedean Stereometry’ and Kepler’s ‘Supplement’; the second, much shorter part (Nos. 69-79), deals almost exclusively with topics from the second part of the Stereometria (problem of the largest cuboid or cylinder in a given sphere; Austrian gauging rod; Austrian barrel and its comparison with barrels of another type, mainly the Rhineland). Part 3 (Nos. 80-90) of the Messekunst, ‘The preparation and use of the Austrian wine gauging rod [Weinvisierrute]’, was based on the third part of the Stereometria. Kepler showed that Austrian barrels are ‘maximal’, in the sense that the accuracy of the method of measurement using the gauging rod is not affected by the different shapes of barrel which result from the extent to which the staves are bent. A new addition to the Messekunst is the metric appendix (Nos. 91-100) [and the Glossary of technical terms]” (Hammer). Kepler omitted from the Messekunst many of the detailed proofs found in the Stereometria, but included numerous examples to compensate. Tables were set up for frequently recurring calculations, such as those for circular arcs, circular sectors, circular segments, and spherical segments. Kepler introduced the use of decimal fractions, using the Bürgi symbolism, in No. 60 and used them consistently from then on – Kepler wrote, for example, 3(65 for what we would write as 3.65; there is only a single decimal fraction in the whole of the Stereometria (Hammer). Kepler omitted from the Messekunst some highly technical results he had included in part 3 of the Nova stereometria concerning the special relations between cylinders and so-called ‘conjugate conical frustums.’ He indicated the correspondence between the two works by means of numerous marginalia in the Messekunst. “According to the wording of the title, it could appear that the Messekunst was only an extract from the Stereometria, aimed at practitioners who could not be expected to provide mathematical proof, with numerous calculated examples and augmented with an appendix on measures and coinage. This view is so widespread that the Messekunst is at best acknowledged as an attempt to form a German mathematical technical language, but hardly as a contribution to stereometry; however, this clearly misses the factual relationship between the two writings. Above all, it should be noted that the Messekunst completes the problem of stereometry in a particularly important way … “[The Appendix on weights and measures] is by no means, as is almost always believed, a mere collection and accumulation of data from the complicated weights and coinage system of the time, but, according to Kepler’s own explanation, aims at a systematization of the units of measurement … This was not a new idea for Kepler. He had already stated it in 1605 in a report for the Archbishop of Cologne, Ernst von Wittelsbach, on the reform of the entire measuring system … Kepler carried this out in the appendix by working out the relations between the individual weights. This was genuinely a task of practical stereometry, not a mere collection of data. “The second, much more important, place where the Messekunst goes beyond the content of the Stereometria is No. 88 … the problem of the incompletely filled or emptied barrel, practically of the same importance as the content calculation of the whole barrel, but much more difficult and above all not to be managed with the gauging rod … Because of its importance, Kepler had tried to solve it in the last chapter of the third part of the Stereometria, but with little luck … “[In the Meesekunst, Kepler] distinguishes the two cases h ≤ b – a and h > b – a, where h is the height of the empty segment, and b and a are the radius of the belly and bottom. If the curvature of the barrel staves is considered to be circular, which is the case to a good approximation, the barrel is a lemon that has been cut at both ends and when h ≤ b – a the resulting segment in Kepler’s language is a lemon wedge. For this he already gave an approximate calculation in No. 67” (Hammer). If h > b – a, the calculation is more difficult but Kepler finally succeeds (see Hammer, pp. 537-538, for an explanation). Exactly the same method was used 150 years later by Johann Heinrich Lambert in Die Visierkunst sowohl ganz als nicht ganz gefüllter liegender Fässer (Beyträge zum Gebrauch der Mathematik und deren Anwendung, Bd. 1 (1765), pp. 314-368). “With this calculation … he puts the crown on his doliometry. Its proper place would have been at the end of the Stereometria, but since Kepler only succeeded in solving the task after the completion of the Latin work, he had to be content with allowing it to appear in the Messekunst … “In the Dissertatio cum Nuncio Sidereo, Kepler wrote a few years earlier: ‘There are people who express their science with a stern expression in order to give weight to their claims … It seems to me that I am naturally designed to alleviate the heavy work of scientific investigation by loosening up the presentation’. This sentence has to be remembered if one wants to correctly judge the ‘Report on the Year of Christ's Birth’ (1613) and the Messekunst, both of which open up the subject of a Latin work to German readers. Both are exemplary instances of good popularization. The Messekunst is about teaching people who have not gone beyond the initial level of geometric and arithmetic knowledge the difficult terminology and calculations of stereometry … The result is a book that still offers enjoyable reading today. However, Kepler had to present a problem which involved many technical terms, for which he needed good German words if he wanted to be understood, but which did not yet exist for stereometry. Only a few examples were available from the German translations of Euclid. In a letter to Nikolaus Vicke in Wolfenbüttel in July 1611, he expressed his opinion on the clarification of technical terminology: ‘Marius teaches Euclid to speak German [in 1609, Simon Marius published the first German translation from the Greek of the Elements] … I struggle with the same task, but my main goal is that the technical terms should also be German’ … The German technical words used or coined by him are compiled by Kepler in a special glossary. Some of these are now a permanent part of mathematical jargon, but the larger part have not prevailed. Nevertheless, the Messekunst remains an important link in the history of German mathematical terminology (cf. A. Gotze, ‘Beginning of a German mathematical terminology by Kepler’, Germanische Studien, Berlin, 1919)” (Hammer). Caspar 49. Parkinson, Breakthroughs, p. 68. Baron, The Origins of Infinitesimal Calculus, 1969. Boyer, The History of the Calculus and its Conceptual Development, 1949. Hammer, ‘Nachbericht,’ in: JohannesKepler Gesammelte Werke IX, 1960. Radelet-de Grave, ‘Kepler, Cavalieri, Guldin. Polemics with the departed,’ pp. 57-86 in: Seventeenth-Century Indivisibles Revisited (Jullien, ed.), 2015. Voelkel, Johannes Kepler and the New Astronomy, 1999.
Folio (298 x 180 mm), pp. [iv], 113, [3, Glossary of technical terms, Register and Errata], with printed slip with woodcut rule on K1r, numerous woodcut diagrams in text (large woodcut on F3v just touched at lower margin by-binder’s knife as almost always, two small paper flaws repaired without loss of text). Contemporary binding using a leaf from a fourteenth-century French canon law text (minor damage to upper part of spine). A very attractive copy.
Item #5003
Price: $25,000.00