Opticks: or, A Treatise of the Reflexions, Refractions, Inflexions and Colours of Light. Also Two Treatises of the Species and Magnitude of Curvilinear Figures.
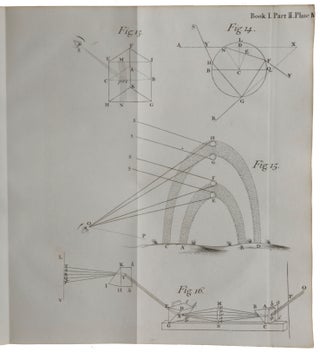
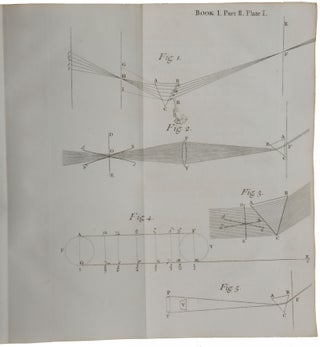
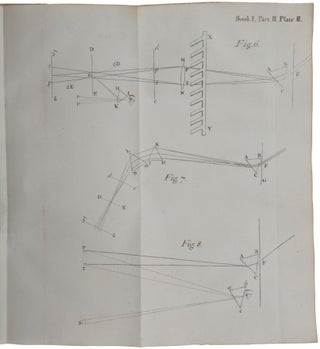
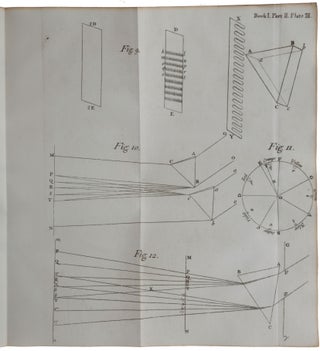
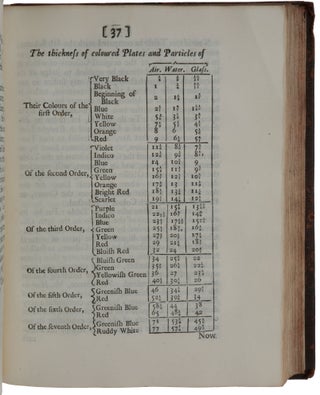
London: Printed for Sam. Smith and Benj. Walford, Printers to the Royal Society, at the Prince’s Arms in St. Paul’s Church-Yard, 1704. First edition, first issue, and a superlative copy, presented by Newton to his close friend and collaborator Nicolas Fatio de Duillier, with an inscription recording the gift in Fatio’s hand and with his ink and pencil annotations in the text. This is the earliest of the six known presentation copies of the Opticks, none of which is inscribed in Newton’s hand – the presentation inscription in this copy is dated five days earlier than that in the copy Newton presented to the Royal Society, of which he was then President. Only one other author’s presentation copy of Opticks has sold at auction, that copy presented to Edmond Halley (lot 918, Robert S. Pirie sale, Sotheby’s New York, December 4, 2015, $1,330,000). Of Newton’s three greatest contributions to science – his theory of gravity, his theories of light and colour, and the invention of calculus – the first was published for the first time in the Principia (1687), and the other two in the present work. “Newton’s Opticks did for light what his Principia had done for gravitation, namely, placed it on a scientific basis” (Babson, p. 66).“One of the supreme productions of the human mind” (Andrade), the Opticks “summarized Newton’s discoveries and theories concerning light and color: the spectrum of the sunlight, the degrees of refraction associated with different colors, the color circle (the first in the history of color theory), the invention of the reflecting telescope, the first workable theory of the rainbow, and experiments on what would later be called ‘interference effects’ in conjunction with Newton’s rings. His discovery of periodicity in Newton’s rings … led Newton to postulate that periodicity was a fundamental property either of light waves or of waves associated with light. Nevertheless, Newton preferred the corpuscular theory of light, with which he is usually associated, because of its explanatory value for certain optical phenomena and because it allowed him to link the action of gross bodies with the action of light” (Norman). “All previous philosophers and mathematicians had been sure that white light is pure and simple, regarding colors as modifications or qualifications of the white. Newton showed that the opposite is true … Natural white light, far from being simple, is a compound of many pure elementary colors which can be separated and recombined at will” (PMM). “Newton’s Opticks dominated the science of optics for over a century … the experimental approach adopted in the Opticks was lauded and widely followed in optical science and served as a model for other experimental sciences” (Shapiro, p. 166). The two appended tracts, Tractatus de quadratura curvarum and Enumeratio linearum tertii ordinis, are the first of Newton’s purely mathematical works to be published. De quadratura is Newton’s first publication of his method of fluxions, or calculus, which he developed in terms of ‘prime and ultimate ratios’, an early version of the theory of limits; it includes the first published statement of the general binomial theorem and of ‘Taylor’s theorem’ on series expansions. Fatio de Duillier, the recipient of this copy of the Opticks, was an accomplished mathematician in his own right. After working in the Netherlands, where he befriended Christiaan Huygens, he came to England in 1687, became a Fellow of the Royal Society in 1688, and made the acquaintance of Newton. Fatio became the leading intermediary between Newton and Huygens; the exchanges between these two great scientists did much to shape and modify Newton’s theories on optics and other matters. In the 1690s, as Newton’s closest confidant, Fatio became the most likely person to oversee a revised edition of the Principia, discussing corrections with Newton and exchanging letters. Fatio championed Newton against his Continental rivals in his Lineae brevissimi descensus investigatio geometrica duplex (1699), the work that ignited the priority dispute with Leibniz over the invention of calculus. The present volume is one of only four books known to survive from Fatio’s library. With the presentation, the close association of author and recipient, the annotations, and the unsophisticated condition of such an important work, this volume could be a centrepiece of even the finest scientific library. Provenance: Inscribed at the top of the front pastedown in Fatio’s hand: “Ex Dono Autoris Clarissimi: Londini, Februarii undecimo, 1703/4. Nicolaus Facius.” Fatio also used the Latin form of his name in an inscription recording presentation by Newton in his copy of the third edition of the Principia (Bodleian Library, Oxford, shelfmark 4° Z. 24 Art.); passed on Fatio’s death to Corfield Clare (d. 1790), rector of Madresfield and of Alvechurch, with whom Fatio lodged; acquired from Clare by James Johnstone (c. 1730-1802), physician and antiquary (bookplate on front paste-down); by descent to John Johnstone (1768-1836), physician in Worcester from 1793 (note of its acquisition by his father on the front free endpaper); bookseller’s pencil notes including a price of £250, dating from before 1971 when the book was acquired by its previous owner. Newton’s studies of light and optics began very early, possibly even before 1665, but were interrupted by the plague, and only resumed two years later. Appointed in 1669 to the Lucasian Chair of Mathematics at Cambridge, he was obliged by the statutes of the post to lecture and to deposit his lectures in the University Library. For the period 1670-1672 Newton lectured on optics and deposited the lectures in October 1674. Although he considered publishing the lectures together with an early tract on calculus, De methodus fluxionum, neither was published until after his death. Newton’s optical work first came to the attention of the Royal Society when Newton exhibited there a telescope he had made. He was elected a fellow shortly thereafter, on 11 January 1672, and responded by offering the Society an account of the discoveries that had led him to his invention. This was his ‘New theory about light and colours,’ published in the Philosophical Transactions on 19 February 1672. In it he described his famous experiments in which sunlight from a tiny hole in a shutter was refracted through a glass prism, resulting in an oblong multi-coloured image on a board opposite. In the ‘experimentum crucis,’ he allowed light of one of the colours into which the sunlight had been separated to pass through a small hole in the board and then to be refracted by a second prism. Newton found that the second prism did not produce any further dispersion of the light, and that rays falling on the second prism with the same angle of incidence suffered unequal degrees of refraction, depending on their colour. He concluded that “Light it self is a heterogeneous mixture of differently refrangible Rays,” and asserted an exact correspondence between colour and “degree of Refrangibility”. Hence, colours “are not Qualifications of Light, derived from Refractions, or Reflections of natural Bodies,” as commonly believed, but “Original and connate properties,” differing in the different sorts of rays. Although Newton presented his theories as being the result of a Baconian induction from experiment, examination of his contemporary notebooks shows that very early in his optical research Newton was explaining his experiments by ‘the corpuscular hypothesis,’ according to which light rays are composed of “very small bodies emitted from shining substances”. In his Philosophical Notebook, probably begun in early 1664, Newton wrote: “Blue rays are reflected more than red rays, because they are slower. Each colour is caused by uniformly moving globuli. The uniform motion which gives the sensation of one colour is different from the motion which gives the sensation of any other colour.” Newton’s great leap forward was actually a consequence of implications drawn from profound scientific speculation and insight. Newton’s ‘New theory’ immediately attracted criticism from Hooke, Huygens, and others. Although Newton initially discounted the idea that light could be a form of wave, as this seemed to contradict the fact that light travels in straight lines, discussions with Huygens resulted in a lengthy ‘Hypothesis Explaining the Properties of Light Discoursed of in my Several Papers,’ in which he supposed that light “is something or other capable of exciting vibrations in the aether,” assuming that “there is an aetherial medium much of the same constitution with air, but far rarer, subtler, and more strongly elastic.” Newton sent the ‘Hypothesis,’ together with a ‘Discourse of Observations,’ in December 1675 to Henry Oldenburg, Secretary of the Royal Society. In the ‘Discourse’, Newton set out “such observations as conduce to further discoveries for completing his theory of light and colours, especially as to the constitution of natural bodies, on which their colours or transparency depend.” It also contained Newton’s account of his discovery of the “rings” produced by light passing through a thin wedge or layer of air between two pieces of glass. He had based his experiments on earlier ones of a similar kind that had been recorded by Robert Hooke in his Micrographia. The ‘Discourse’ was, in fact, an almost verbatim draft of parts I, II and III of Book II of Opticks, and in 1676 Newton briefly considered publishing it, but in the end this came to nothing. Book II, part IV seems to have been drafted in 1681, but, as we shall see, the material in part IV appeared in a different form in the Opticks. Newton’s interests now turned to alchemy, and then from 1684 to the composition of Principia. Only after its publication did Newton return to his optical work. “Newton wrote most of the Opticks between 1687 and early 1692. He wrote Book I, Parts I and II, expounding his new theory of light and colour, in 1687. He then appears to have set aside the Opticks for about three years, but by the late summer or autumn of 1691, he had considered it – at least for a few months – to be complete. It is most likely that he carried out new research and wrote the remainder of the Opticks – that is, Books II and III – in the winter or spring of 1692, or perhaps six months earlier. At some time between late August 1691 and late February 1692, Newton decided to revise the draft significantly. After this effort he brought it close to its published form except for the brief last book on diffraction [which Newton called ‘inflexion’] and the queries which were not prepared for publication until shortly before publication in 1704. “The composition of Book II in 1690 or 1691 at first went very quickly. Newton made so few changes in the text that he was able to mark up the manuscript of the [‘Discourse of] Observations’ from 1675 for his amanuensis to copy for the Opticks. This formed Parts I and II and much of Part III … After revising the ‘Observations’, Newton was confronted with a decision on how to end his book. At first he planned to follow this material with a new fourth book or part on diffraction, but he was also toying with the idea of a speculative ‘Fourth Book’. Newton soon reined in his more speculative tendencies and turned to more empirical optical investigations. He continued experiments on diffraction and also discovered an entirely new phenomenon: coloured rings produced in transparent thick plates. By the autumn of 1691, Newton had completed and written up his investigations of thick plates as Book IV, Part I, which, together with his research on diffraction, Book IV, Part II, was to form the concluding book of the Opticks. “Between late August 1691 and late February 1692, Newton removed the two parts of the new Book IV from the manuscript and set about revising them. The part on diffraction was troublesome and remained incomplete until shortly before publication. Within six months, however, he revised the part on the colours of thick plates, incorporated it into Book III because of their affinity to those of thin films, and essentially put it into its published state. During this revision, Newton also introduced his theory of fits – an immaterial vibration to explain the physical cause of periodicity in light that replaced his earlier aetherial and corpuscular vibrations” (Shapiro, pp. 187-188). On 15 November 1702, according to a memorandum by the Scottish mathematician and Oxford Professor of Astronomy David Gregory, Newton “promised Mr Roberts, Mr Fatio, Capt. Hally & me to publish his Quadratures, his treatise of Light, & his treatise of the Curves of the 2d Genre” [i.e., cubic curves]. The book appeared by 16 February 1704, when Newton presented a copy to the Royal Society” (ibid., p. 196). The copy on offer was presented to Fatio five days earlier. In the published work, “Newton presented his main discoveries and theories concerning light and color in logical order, beginning with eight definitions and eight axioms … Eight propositions follow, the first stating that ‘Lights which differ in Colour, differ also in Degrees of Refrangibility.’ In appended experiments Newton discussed the appearance of a paper colored half red and half blue when viewed through a prism and showed that a given lens produces red and blue images, respectively, at different distances. The second proposition incorporates a variety of prism experiments as proof that ‘The Light of the Sun consists of Rays differently refrangible.’ “The figure given with experiment 10 of this series illustrates ‘two Prisms tied together in the form of a Parallelopiped’. Under specified conditions, sunlight entering a darkened room through a small hole F in the shutter would not be refracted by the parallelopiped and would emerge parallel to the incident beam, from which it would pass by refraction through a third prism, which would by refraction ‘cast the usual Colours of the Prism upon the opposite Wall.’ Turning the parallelopiped about its axis, Newton found that the rays producing the several colors were successively ‘taken out of the transmitted Light’ by ‘total Reflexion’; first ‘the Rays which in the third Prism had suffered the greatest Refraction and painted [the wall] with violet and blew were … taken out of the transmitted Light, the rest remaining,’ then the rays producing green, yellow, orange, and red were ‘taken out’ as the parallelopiped was rotated yet further. Newton thus experimentally confirmed the ‘experimentum crucis,’ showing that the light emerging from the two prisms ‘is compounded of Rays differently Refrangible, seeing [that] the more Refrangible Rays may be taken out while the less Refrangible remain’ … In proposition 6 Newton showed that, contrary to the opinions of previous writers, the sine law [of refraction] actually holds for each single color. The first part of book I ends with Newton’s remarks on the impossibility of improving telescopes by the use of color corrected lenses and his discussion of his consequent invention of the reflecting telescope. “In the second part of book I, Newton dealt with colors produced by reflection and refraction (or transmission), and with the appearance of colored objects in relation to the color of the light illuminating them. He discussed colored pigments and their mixture and geometrically constructed a color wheel, drawing an analogy between the primary colors in a compound color and the “seven Musical Tones or Intervals of the eight Sounds, Sol, la, fa, sol, la, mi, fa, sol….” “Proposition 9, ‘Prob. IV. By the discovered Properties of Light to explain the Colours of the Rain-bow,’ is devoted to the theory of the rainbow. Descartes had developed a geometrical theory, but had used a single index of refraction in his computation of the path of light through each raindrop. Newton’s discovery of the difference in refrangibility of the different colors composing white light, and their separation or dispersion as a consequence of refraction, on the other hand, permitted him to compute the radii of the bows for the separate colors. He used 108:81 as the index of refraction for red and 109:81 for violet, and further took into consideration that the light of the sun does not proceed from a single point. He determined the widths of the primary and secondary bows to be 2°15' and 3°40', respectively, and gave a formula for computing the radii of bows of any order n (and hence for orders of the rainbow greater than 2) for any given index of refraction … “Book II, which constitutes approximately one third of the Opticks, is devoted largely to what would later be called interference effects, growing out of the topics Newton first published in his 1675 letter to the Royal Society. Newton’s discoveries in this regard would seem to have had their origin in the first experiment that he describes (Book II, Part 1, Observation 1); he had, he reported, compressed ‘two Prisms hard together that their sides (which by chance were a very little convex) might somewhere touch one another’ (as in the figure provided for Experiment 10 of Book I, Part 1). He found ‘the place in which they touched’ to be ‘absolutely transparent,’ as if there had been one ‘continued piece of Glass,’ even though there was total reflection from the rest of the surface; but ‘it appeared like a black or dark spot, by reason that little or no sensible light was reflected from thence, as from other places’ … Rotating the two prisms around their common axis (Observation 2) produced ‘many slender Arcs of Colours’ which, the prisms being rotated further, ‘were compleated into Circles or Rings.’ In Observation 4 Newton wrote that ‘To observe more nicely the order of the Colours … I took two Object-glasses, the one a Plano-convex for a fourteen Foot Telescope, and the other a large double Convex for one of about fifty Foot; and upon this, laying the other with its plane side downwards, I pressed them slowly together, to make the Colours successively emerge in the middle of the Circles, and then slowly lifted the upper Glass from the lower to make them successively vanish again in the same place.’ It was thus evident that there was a direct correlation between particular colors of rings and the thickness of the layer of the entrapped air … Furthermore, as he noted in Observation 13, ‘the Circles which the red Light made’ were ‘manifestly bigger than those which were made by the blue and violet’ … He concluded that the rings visible in white light represented a superimposition of the rings of the several colors, and that the alternation of light and dark rings for each color must indicate a succession of regions of reflection and transmission of light, produced by the thin layer of air between the two glasses … “Book II, Part 2, of the Opticks has a nomogram in which Newton summarized his measures and computations and demonstrated the agreement of his analysis of the ring phenomenon with his earlier conclusions drawn from his prism experiments – ‘that whiteness is a dissimilar mixture of all Colours, and that Light is a mixture of Rays endued with all those Colours.’ The experiments of Book II further confirmed Newton’s earlier findings ‘that every Ray have its proper and constant degree of Refrangibility connate with it, according to which its refraction is ever justly and regularly perform’d,’ from which he argued that ‘it follows, that the colorifick Dispositions of Rays are also connate with them, and immutable.’ The colors of the physical universe are thus derived ‘only from the various Mixtures or Separations of Rays, by virtue of their different Refrangibility or Reflexibility’; the study of color thus becomes ‘a Speculation as truly mathematical as any other part of Opticks.’ “In Part 3 of Book II, Newton analyzed ‘the permanent Colours of natural Bodies, and the Analogy between them and the Colours of thin transparent Plates.’ He concluded that the smallest possible subdivisions of matter must be transparent, and their dimensions optically determinable. A table accompanying Proposition 10 gives the refractive powers of a variety of substances ‘in respect of … Densities.’ Proposition 12 contains Newton’s conception of ‘fits’: ‘Every Ray of Light in its passage through any refracting Surface is put into a certain transient Constitution or State, which in the progress of the Ray returns at equal Intervals, and disposes the Ray at every return to be easily transmitted through the next refracting Surface, and between the returns to be easily reflected by it.’ The succeeding definition is more specific: ‘The returns of the disposition of any Ray to be reflected I will call its Fits of easy Reflection, and those of its disposition to be transmitted its Fits of easy Transmission, and the space it passes between every return and the next return, the Interval of its Fits.’ The ‘fits’ of easy reflection and of easy refraction could thus be described as a numerical sequence; if reflection occurs at distances 0, 2, 4, 6, 8, …, from some central point, then refraction (or transmission) must occur at distances 1, 3, 5, 7, 9, …. Newton did not attempt to explain this periodicity, stating that ‘I do not here enquire’ into the question of ‘what kind of action or disposition this is’ … Newton thus integrated the periodicity of light into his theoretical work … His work was, moreover, based upon extraordinarily accurate measurements – so much so that when Thomas Young (1773-1829) devised an explanation of Newton’s rings based on the revived wave theory of light and the new principle of interference, he used Newton’s own data to compute the wavelengths and wave numbers of the principal colors in the visible spectrum and attained results that are in close agreement with those generally accepted today. “In Part 4 of Book II, Newton addressed himself to ‘the Reflexions and Colours of thick transparent polish’d Plates.’ This book ends with an analysis of halos around the sun and moon and the computation of their size, based on the assumption that they are produced by clouds of water or by hail. This led him to the series of eleven observations that begin the third and final book, ‘concerning the Inflexions of the Rays of Light, and the Colours made thereby,’ in which Newton took up the class of optical phenomena previously studied by Grimaldi, in which ‘fringes’ are produced at the edges of the shadows of objects illuminated by light ‘let into a dark Room through a very small hole.’ Newton discussed such fringes surrounding the projected shadows of a hair, the edge of a knife, and a narrow slit” (DSB). “Since Newton published the Opticks without a complete investigation into diffraction, which he had hoped would support a corpuscular theory of light in which light corpuscles were acted on by short-range forces of matter” (Shapiro, p. 196), “Newton concluded the first edition of the Opticks with a set of sixteen queries, introduced ‘in order to a further search to be made by others.’ He had at one time hoped he might carry the investigations further, but was ‘interrupted,’ and wrote that he could not ‘now think of taking these things into farther Consideration.’ In the eighteenth century and after, these queries were considered the most important feature of the Opticks … The original sixteen queries at once go beyond mere experiments on diffraction phenomena. In Query 1, Newton suggested that bodies act on light at a distance to bend the rays; and in Queries 2 and 3, he attempted to link differences in refrangibility with differences in ‘flexibility’ and the bending that may produce color fringes. In Query 4, he inquired into a single principle that, by ‘acting variously in various Circumstances,’ may produce reflection, refraction, and inflection, suggesting that the bending (in reflection and refraction) begins before the rays ‘arrive at the Bodies.’ Query 5 concerns the mutual interaction of bodies and light, the heat of bodies being said to consist of having ‘their parts [put] into a vibrating motion’; while in Query 6 Newton proposed a reason why black bodies ‘conceive heat more easily from Light than those of other Colours.’ He then discussed the action between light and ‘sulphureous’ bodies, the causes of heat in friction, percussion, putrefaction, and so forth, and defined fire (in Query 9) and flame (in Query 10), discussing various chemical operations. In Query 11, he extended his speculations on heat and vapors to sun and stars. The last four queries (12 to 16) of the original set deal with vision, associated with ‘Vibrations’ (excited by ‘the Rays of Light’) which cause sight by ‘being propagated along the solid Fibres of the optick Nerves into the Brain.’ In Query 13 specific wavelengths are associated with each of several colors. In Query 15 Newton discussed binocular vision, along with other aspects of seeing, while in Query 16 he took up the phenomenon of persistence of vision” (DSB). “Newton’s inability to conclude the part on diffraction that he had removed from the first completed state of the Opticks was a principal reason that its publication was delayed for twelve years until 1704. The manuscripts related to the Opticks allow us to identify the cause of Newton’s problem. He had developed a model of diffraction that assumed that the paths of the fringes were identical to, or coincided with, the rectilinear paths of the rays that produced them, but then carried out an experiment that conclusively refuted this assumption. Newton first learned about diffraction from Hooke’s account at a meeting of the Royal Society in 1675, but he only dabbled with the phenomenon until he carried out a serious experimental investigation in 1690-91 … In 1696, Newton left Cambridge for London to assume his duties of Warden of the Mint. He no longer had the time and apparently the interest to resume his experiments on diffraction. The Opticks in Newton’s eyes was still incomplete. Newton could not yet accept publishing the Opticks without the part on diffraction. According to the traditional account, Newton delayed the publication of the Opticks until after Hooke’s death in March 1703, because he feared yet another dispute with him. The principal reason for the delay, however, was that there was no Opticks to publish. It was incomplete. Until the late 1690s Newton evidently intended to return to his diffraction experiments. He was certainly fearful of another round of controversy as he affirmed in his correspondence and in the Advertisement to the Opticks: ‘To avoid being engaged in Disputes about these Matters, I have hitherto delayed the Printing, and should still have delayed, had not the importunity of Friends prevailed upon me.’ Yet, neither Newton nor any of his contemporaries specifically mentioned Hooke” (Shapiro, pp. 193-195). Hooke’s last years were almost entirely consumed by concerns about his own deteriorating health, and he was in no state to trouble Newton as he had in the past. Newton appended to the Opticks two mathematical tracts, of which the first, Tractatus de quadratura curvarum, is Newton’s first published account of the calculus of fluxions. In Newton’s time, finding the ‘quadrature’ of a curve meant finding the area enclosed or subtended by it, which for us is a problem of integral calculus and for Newton one of the ‘inverse method of fluxions’. Newton wrote three extended treatises on fluxions. The first of these, ‘De analysi per aequationes numero terminorum infinitas,’ was composed in 1669 and treats Newton’s general methods of infinite series. It was not published until 1711, when William Jones included it, along with a number of other tracts, in his Analysis per quantitatum series. In ‘De analysi,’ however, Newton “did not explicitly make use of the fluxionary notation or idea. Instead, he used the infinitely small, both geometrically and analytically, in a manner similar to that found in Barrow and Fermat, and extended its applicability by the use of the binomial theorem” (Boyer, The Concept of Calculus, p. 191). It was in the second of Newton’s calculus treatises, ‘De methodus fluxionum’, composed in 1671 but not published until 1736, that he first “introduced his characteristic notation and conceptions. Here he regarded his variable quantities as generated by the continuous motion of points, lines, and planes, rather than as aggregates of infinitesimal elements, the view which had appeared in ‘De analysi’. … In the ‘Methodus fluxionum’ Newton stated clearly the fundamental problem of the calculus: the relation of quantities being given, to find the relation of the fluxions of these; and conversely” (ibid., pp. 192-3), i.e., the processes that we call differentiation and integration. De quadratura was the first of Newton’s treatises on fluxions to be published, but the last to be composed, so that it represents his most mature view of the subject. It was prompted by a letter from David Gregory, on 7 November 1691, sending Newton “my method of squaring figures, published three years ago but now clarified by examples. If only I might be allowed to know your method too, which, as I have subsequently gathered, differs little from mine.” “By late December, Newton’s new tract was already far enough advanced to completion for him to tell Gregory at the beginning of a three-week visit he made to London that he planned to publish it … In the course of the same visit he likewise informed Fatio de Duillier more vaguely that his ‘treatise of curves would soon see the light.’ A month afterwards, having looked through the text of ‘De quadratura’ himself, Fatio could report to Christiaan Huygens that it compared with Leibniz’ letters and publications on ‘Calculus differentialis’ like a ‘finished original’ to a ‘lame and very imperfect copy,’ adding that ‘what he has on quadratures is infinitely more general than all that has been had before, and it is very simple and of wonderful use in all parts of geometry’ (Fatio to Huygens, 15 February 1692). Four weeks later, he added vividly if with exaggeration that ‘I have been chilled to see what Mr Newton has done, and have reproached him for rendering my own hard work useless and not wanting to leave anything for his friends who are come after him to do’ (ibid., 17 March). But by then, as Fatio sadly admitted in the same letter to Huygens, the heat of Newton’s interest in seeing his treatise into print was past and his attention had already strayed to other matters” (Papers VII, pp. 11-13). In the 1691/92 manuscript, Newton went so far as to include a recognition of Fatio’s contributions, not to editorial duties, but to the work itself. This “occurs in [Newton]’s acknowledgement – in itself unusual – regarding the employment of a multiplying factor to reduce a given first-order fluxional equation to directly quadrable form that ‘This rule, or one like it, was communicated to me some time ago by Mr Fatio’” (ibid., p. 14). Not just unusual, it was unprecedented – according to Westfall (Never at Rest (1980), p. 516), “one will look in vain for a similar passage elsewhere in Newton’s mathematical papers.” “The work is significant in a number of ways. At the level of notation the manuscript of 1691-2 saw for the first time the use of Newton’s dotted fluxional notation. The notation was preserved in the published version of De quadratura. Also used was a capital Q to stand for the process of quadrature, rather than the summation sign ∫ adopted by Leibniz in his published work. On a more substantive issue, De quadratura contained the first published statement of the binomial theorem, discovered by Newton some forty years before. The text of De quadratura, in its published form, is in two parts. In the first part Newton, in the manner of De analysi, demonstrated how infinite series could be deployed to determine the quadrature and rectification of curves. In the second part he returned to the topic of fluxions, discussed at greater length in his then unpublished De methodis [eventually published as The method of fluxions and infinite series in 1736]” (Gjertsen, p. 579). But perhaps “Newton’s most important achievement in his ‘De quadratura’ [was] the first explicit enunciation of the Taylor expansion of a general function – Newton deduced the particular ‘Maclaurin’ form in his Corollary 3 (by successive differentiation, it would seem) and then passed to the general theorem in his Corollary 4” (Papers VII, pp. 18-19). The expansion was rediscovered by Brook Taylor in 1715. The second appended mathematical treatise, Enumeratio linearum tertii ordinis, was composed in summer 1695, although it was based on researches carried out intermittently over the previous three decades. “In some ways the Enumeratio is the most original of Newton’s mathematical works. It had no predecessors, met with no rivals claiming to have anticipated the results, or few even who acknowledged its results” (Gjertsen, p. 187). Since the inception of analytic geometry – most notably with Descartes’s Géométrie (1637), which Newton carefully studied in its Latin translation (1659-61) – European mathematicians became interested in the algebraic representation of plane curves. As Descartes showed, and John Wallis further developed, conic sections can be represented by second-degree polynomial equations in two variables (in Cartesian coordinates, as we would say nowadays), and they can be divided into circle, parabola, ellipse and hyperbola. The question naturally arises of how to move a step further and study the graphs of third-degree polynomials. In the Enumeratio, Newton gave a classification of cubic curves analogous to the classification of conic sections. He identified 72 species of cubic curves, mostly classified in terms of the properties of their diameters and asymptotes. There are, in fact, 78 species: four were added by James Stirling in his Lineae tertii ordinis Newtonianae (1717), and the remaining two by François Nicole and Nicolas I Bernoulli in the 1730s. Newton uses oblique Cartesian axes (something Descartes did not do) and has no qualms in using negative coordinates (a novelty at the time). Newton also demonstrates deep geometrical insights, stating a general theorem according to which all cubic curves can be obtained by centrally projecting the five ‘divergent parabolas’, very much as all conics can be obtained by projecting the circle; this was proved by Nicole and Alexis-Claude Clairaut in 1731. In the final section of the work, Newton shows how the real roots of polynomial equations of degree up to 9 can be found from the points of intersection of cubic curves with lines, conics or other cubic curves. Newton gave almost no proofs of his claims but Stirling revealed the methods Newton had used: algebra and infinite series. Newton’s published treatise is “a marvellous epitome of results whose subtleties were only just becoming to be understood by mathematicians in the last decade of Newton’s life, half a century after their initial discovery” (Papers VII, p. 588 n1). Fatio’s copy of the Opticks is of the first issue, without Newton’s name on the title page. In fact, the author identifies himself only by the initials ‘I. N.’ at the end of the preface. “The omission of the author’s name, like the choice of English rather than Latin as the language of the text, would seem to be a kind of admission by Newton of the imperfect or incomplete nature of the Opticks and was to some degree an echo of the failure to produce a mathematical treatise or at least a treatise on optics based on mathematical principles” (Cohen, p. 41). A second issue, with the title page printed entirely in black and bearing Newton’s name in full, but otherwise identical to the first issue, is known in two copies (British Optical Association and Babson – the mathematical treatises are lacking in the latter copy). That this issue is indeed the second is confirmed by the fact that the title is a cancel in both of the known copies. “Evidently, the printer (or someone else) decided that there should be at least one copy of record, identifying the author by giving his name in full” (Cohen, p. 40). Nicolas Fatio de Duillier (1664-1753) was a Swiss mathematician and natural philosopher. Educated at the Academy of Geneva, Fatio worked with Giovanni Domenico Cassini at the Royal Observatory in Paris in the early 1680s. He first came to England in 1687 and became a Fellow of the Royal Society on 2 May 1688. After the Revolution of 1688, Fatio was the most important intermediary between Newton and Huygens. Fatio regarded himself (with some justification) as being among the very few mathematicians internationally who were equipped to handle the new calculus and as being in the forefront of scientists who were trying to explain the action of gravity, the force which played such an important role in the physical explanations provided by the Principia. When in the later spring of 1689 Huygens paid his first visit to England, Fatio escorted his friend about the capital. He was also present at the meeting of the Royal Society on 12 June at which Huygens and Newton met for the first time; this may also have been the occasion of Fatio’s introduction to Newton. Fatio soon expressed his veneration for Newton, “the most honourable man I know, and the ablest mathematician who has ever lived” (Westfall, p. 493). His scrutiny of Principia convinced Fatio of the failure of all theories of gravity based upon Cartesian vortices. In March 1690 Fatio presented his own theory of gravity to the Royal Society. Two days later Newton came to London and spent a month in Fatio’s company, during which they studied Huygens’ recently published Traité de la Lumière, which also contained Huygens’ views on gravity. After a brief visit to the Netherlands, where he visited Huygens, Fatio returned to England in September 1691 and immediately resumed contact with Newton. Fatio soon emerged as the likeliest person to produce a revised edition of the Principia and discussed corrections to the work with Newton, to whose manuscripts he also had access. At this time, he was one of Newton’s closest confidants. The two men regularly exchanged letters (several of which remain unpublished) and Fatio advised Newton in particular about the purchase of alchemical works in French. For much of 1693, Newton and Fatio collaborated on alchemical experiments, with Fatio conveying information derived from practitioners with whom he associated in the London Huguenot community. According to William R. Newman, who has recently produced a definitive account of the alchemical collaboration of Newton and Fatio, Newton was “testing the ability of a vitriol to ‘ferment’ respectively with salts of lead, tin, and copper” and fermenting iron, copper, and lead with metallic quicksilver. Exhaustion from long hours tending the furnace involved in these experiments may well have caused Newton’s famous breakdown, which he discussed in letters to Samuel Pepys and John Locke in autumn 1693. Newman’s work demonstrates that Fatio’s involvement with Newton reflected shared intellectual concerns with “chymistry, the transformation of materials, and the production of remedies.” These interests remained vital despite Newton’s illness, which cannot now be attributed to any falling out with Fatio. Fatio found new employment as a tutor in 1694, which required him to be away from London; he travelled to the Netherlands with his pupil in 1697-8, and returned to Geneva between 1699 and 1701. Nevertheless, he remained a regular participant in conversations among Newton and his disciples: his interest in the renewed editing of the Principia and in Newton’s other projects was taken for granted. In London in 1698, Fatio set to work seeing two compositions of his own through the press: an English treatise on the exploitation of the angle of the sun’s rays in gardening (Fruit Walls Improved), a work which had a small but lasting influence on the history of photometry; and a Latin pamphlet on the geometrical investigation of the line of quickest descent (Lineae brevissimi descensus), a work notable for its author’s attempt to reassert a position among the front rank of European mathematicians. As such Fatio was critical of the behaviour of Johann Bernoulli and his associates for the nature of the challenge problem which they had issued in 1696, and which Newton had answered with a correct solution for the line of quickest descent. Newton had presented his work anonymously in the Philosophical Transactions (January 1697), but gave no hint about the method he had followed. He presented a construction of the solution-curve (a cycloid). Behind Bernoulli’s challenge lurked Gottfried Wilhelm Leibniz, whom Fatio accused of having ignored Newton’s priority in the invention of the calculus in his publications about this mathematical tool. At the heart of the dispute lay a broader intellectual problem that many Continental mathematicians had in accepting Newton's subordination of his method of fluxions to traditional geometrical arguments and their consequent belief that Newton had not properly mastered the intricacies of the new analysis that Leibniz had developed. On such a reading, no other mathematician in England except Newton was worthy of consideration (Fatio included). Fatio’s pamphlet also treated the problem of the solid of least resistance, which Newton had solved in Book II of the Principia. He wished to show that, since Newton had solved the problem of the solid of least resistance in 1687, he could equally well solve the problem (belonging to the same class) of the line of quickest descent nine years later. Mathematically speaking the two problems are similar: if you know how to solve one, then you are likely to know how to solve the other. Fatio’s work therefore set out to suggest that, since he and Newton had known one another and shared mathematical work since 1687, he too rightfully belonged among the sharpest mathematicians of Europe. Fatio’s publication is properly considered the opening salvo in a decade and a half of philosophical warfare between Newton and Leibniz. Although Leibniz and Johann Bernoulli were critical of Fatio’s own solutions to the problem of the line of quickest descent, other leading mathematicians such as Jakob Bernoulli or Jakob Hermann were far more circumspect. They were particularly interested in the explanation of the mechanism of gravity that Fatio shared with them as part of his exchanges at this time. Fatio had presented these ideas to the Royal Society as early as July 1688, but they remained topical as Continental mathematicians and philosophers struggled to interpret the Principia. In this way, Fatio’s pamphlet succeeded in reclaiming attention for his own scientific ideas, as well as going into the lists for Newton's reputation. It also showed that he could handle the most difficult problems in mathematics. By the time of his return from Switzerland in 1701, Fatio was therefore a significant player in an international debate about the nature of the calculus and about the way in which physical effects might be transmitted so as to appear to cause action at a distance. These were also concerns looked at in the Opticks, initially in the two mathematical tracts appended by Newton to the work, and later also in the queries that were developed from Newton’s theory of light in the revisions made to the Latin translation (Optice) of 1706. At the same time, Fatio re-established himself as a contact between Newton and skilled craftsmen in the London Huguenot community, as is shown by exchanges between the two men in the year of publication of the Opticks. These concerned the design of watches with a jewelled mechanism, which Newton eventually tested for accuracy in December 1704. Finally, Newton was in Fatio’s debt as the recipient of a presentation copy of Fatio’s own publication of 1699. It is not surprising therefore to find that Fatio was one of the very first recipients of a presentation copy of the Opticks on 11 February 1704. Newton’s gift of the Opticks to Fatio and the close reading implied by Fatio’s annotations formed part of a broader pattern of gift-giving. Halley presented Fatio with a copy of the first edition of the Principia in 1687 (now Bodleian Library, Oxford, shelfmark Arch. A d.37). Fatio reciprocated by presenting his own book to both Newton and Halley. Newton responded with a copy of the Opticks. Fatio was an attentive enough reader of the mathematical treatises appended to the book to make a small number of accurate corrections which were not in the errata. The mathematical tracts appended to the Opticks included some of Newton’s most profound analysis of the quadrature of curves and of cubic curves, the culmination of work that he had begun in the mid-1660s and perfected in the mid-1690s. As such they had direct relevance to the growing public quarrel into which Fatio had pitched Newton. Fatio discussed the content of the Opticks with his correspondents on the Continent, although only after the latter had been able to read the work in Latin. His ongoing interest in solar light and “crowns of colours wch sometimes appear about the Sun & Moon” was the subject of a letter that Newton sent to Fatio on 14 September 1724, offering to communicate his ideas to the Royal Society. Fatio’s copy of the Opticks is largely invisible in scholarship, although its possible existence is mentioned in Charles Domson’s thesis ‘Nicolas Fatio de Duillier and the Prophets of London’ (Yale University, 1972, p. 84). Fatio died in Worcester, where he had lived since 1717, in April 1753. Half of his effects passed to Corfield Clare (d. 1790), rector of Madresfield and of Alvechurch, with whom he had lodged. The other half was bequeathed to the widow of Jean Allut (1682-1739), who was, like Fatio, a disciple of the enthusiastic Camisard prophets who had come to England in 1706. In April 1765, the Genevan natural philosopher George-Louis Le Sage purchased for £8 some of the papers that had been left to Clare. What remained in Worcestershire was acquired by the physician and antiquary James Johnstone (c. 1730-1802). His son, John Johnstone (1768-1836), who practised medicine in Worcester from 1793, later inherited the Opticks (and made a note of its acquisition by his father on the front free endpaper). He also owned other books and papers that had belonged to Fatio (most of which are now impossible to locate). John Johnstone became a Fellow of the Royal Society in 1815 and subsequently donated Fatio’s notes on the revision of the Principia to the Society’s library. Two books from Fatio’s library (copies of the first and the third edition of the Principia) survive in the Bodleian Library, Oxford, but they had presumably been sold by either Clare or Mrs Allut immediately after Fatio’s death, since they were acquired from an Oxford bookseller in 1755. The Bodleian also owns a copy of Some Manifestations and Communications of the Spirit (London, 1730), a work associated with the French Prophets, which has annotations made by Fatio in Worcester in 1731. This book belonged shortly after Fatio’s death to Sir John Van Hatten of Dinton Hall, Buckinghamshire, but in the twentieth century had an American owner before being purchased by the Bodleian. The Opticks has no direct sign of provenance after John Johnstone. It does bear one or two booksellers' marks and a price (£250/0/0) indicating that it was sold in England before 1971. The print-run of the first edition of the Opticks is unknown. From the later records in the Bowyer ledgers for other books by Newton (including the second edition of the Opticks), it seems fair to assume an edition size of between 750 and 1,000 copies. The Babson catalogue lists 35 institutional copies of the first edition of the Opticks. Wallis lists 59 with a further two of the second issue. ESTC gives 129 institutional holdings (two of which are in fact duplicated), without differentiating the two issues. With the use of additional databases and the consultation of individual online catalogues to confirm the status of particular copies, it is straightforward to identify at least 185 surviving copies, together with one copy (from those identified by Wallis) that was destroyed in the Second World War. Of these 185 copies, it has been possible to establish provenance data and descriptions of condition for approximately thirty-five for the purposes of comparison. Most of these copies are bound in Cambridge-style panelled calf with blind fleurons on the boards. This may reliably be assumed to have been a publisher's binding, although the spine decoration may not always have been standard (many copies have been rebacked or otherwise altered). That said, copies in unrestored, original condition (such as Edmond Halley’s copy, John Locke’s copy, or the copy in the Old Library of Magdalene College, Cambridge) have identical decoration, tooling, and lettering on boards, spine, and (where present) red morocco spine label (gilt lettering: NEWTON’S | OPTICKS | &c). Very few surviving copies have extensive contemporary annotations: exceptions include the copies that belonged to Newton himself (Cambridge University Library, shelfmark Adv.b.39.4, used to prepare the second edition of 1717 [lacking title-page and all after p. 137 in Book III]; Trinity College, Cambridge, shelfmark NQ.16.198 [lacking pp. 1-17 and the mathematical treatises], and McGill University Library, Montreal, MS 46 [shelfmark QC353.N57.1704]) or the copy in the Boston Public Library (with contemporary corrections and additions not in Newton's hand, giving cross-references to the work of his Cambridge successor, William Whiston). There are a number of copies with annotations from the later eighteenth or nineteenth centuries (e.g. that at the Senate House Library, London, with the annotations of the mathematician and biographer of Newton, Augustus De Morgan). There are also a number of copies that can be identified with provenance at or near to the date of publication. Among these is a copy bought by Francis Cremer [presumably of Ingoldisthorpe, Norfolk (d. 1759)] for 12s. in 1704, and one of the copies formerly at the Babson Institute (now on deposit in the Huntington Library, San Marino, California), which has a manuscript price code with the date 1704. Leibniz’s copy (Gottfried-Wilhelm-Leibniz Bibliothek, Hannover) was sent to him from London by John Hutton on 2 May (13 May NS) 1704 and received in Hannover via The Hague before 22 July (NS). The Opticks was published after the death of Samuel Pepys in 1703, but a copy entered his library during the period in which it was being curated by his nephew, John Jackson (before 1705). The French physician, Etienne François Geoffroy, received a copy (now in Cornell University Library), from Hans Sloane (Secretary to the Royal Society) via the Jesuit mathematician, Jean de Fontenay. Fontenay had visited London, where he presented Chinese artefacts to the Royal Society in March 1704. Geoffroy thanked Sloane for the gift in a letter of 20 January 1706 (NS) and presented a summary of the book’s contents to the Académie Royale des Sciences in a series of sessions between 7 August 1706 and 1 June 1707. The first copy that can be traced as arriving in North America was given by James Peirce to the Library of Harvard College on 30 March 1706 (now in the Houghton Library). More interesting still are copies presented to their first owners by Newton himself (none of which bear inscriptions in Newton’s own hand). These include: Many of Fatio’s annotations deal with errors already described on the errata page of the Opticks (where Fatio notes that he has corrected these errata in the text: ‘Haec Errata correcta sunt’). Most are in ink, some are in pencil. The pencil corrections, which are confined to De Quadratura, are all found in the 1711 edition of Newton’s mathematical tracts and were presumably added after that date. The ink corrections are more likely to have been made shortly after Fatio was given the book, although some of them may have been incorporated from the 1706 Latin Optice, in which they also appear. There is no evidence of any communication between Newton and Fatio in the making of these corrections. The only one of Newton’s copies of the Opticks to contain the mathematical tracts is now at McGill University. It contains only one of the corrections made by Fatio in pencil, but it also contains many other corrections and additions incorporated either in the 1706 Optice or in the 1711 mathematical tracts which are not in Fatio’s copy of the Opticks. The errata are mostly corrected in the main body of the text in all three of Newton’s copies of the Opticks. In the copy at Trinity College, these corrections are frequently not in Newton’s hand, suggesting that they were made already in the printing shop. In Fatio’s copy, occasional items in the errata have not been corrected in the text (e.g. the corrections for pp. 86, 93, and one of those for p. 143 in book I, pp. 11 (in fact, a mistake in the errata); pp. 96, 101 (where the wrong number is corrected by Fatio) in book II). Despite such slips, the annotations show Fatio as an attentive and mathematically literate reader of the Opticks. This copy is the earliest witness to the publication of the Opticks and a valuable testament to the ongoing friendship and intellectual exchange between Newton and Nicolas Fatio de Duillier, a very significant figure in his own right and the first mover in the public calculus controversy. It is one of only four books known from Fatio’s library and is undoubtedly the most significant book that could emerge that he owned. It is a more interestingly annotated copy of the Opticks than any of the other surviving presentation copies (including that given to Halley) or than most of the other copies (apart from Newton’s own) with contemporary annotations and provenance. Of known presentation copies that cannot now be located, Grandi’s would not compare with Fatio’s for interest or significance, Other copies that might be presumed to have existed include that of John Flamsteed (acquired by November 1704, but unknown apart from references in correspondence) and that of David Gregory. Because the book was in English, most important Continental contemporaries of Newton (such as the Bernoullis) did not acquire it until after the publication of the Latin Optice in 1706. None of these copies, were they to come onto the market, would surpass Fatio’s unless they were very heavily annotated with original material. Moreover, Fatio’s copy is in good, original condition and compares very well in this respect with any other copy that is available or likely to become available. Babson 132; Becker 172 (“The classical formulation and first full presentation of Newton's corpuscular or emission theory of light”); Burchett, p. 17-18; Dibner, Heralds of Science 148; Gray 174; Grolier/Horblit 79b; Norman 1588; Sparrow, Milestones of Science 150; PMM 172; Wallis 174. Gjertsen, The Newton Handbook, 1986. Shapiro, ‘Newton’s Optics,’ pp. 165-198 in: The Oxford Handbook of the History of Physics (Buchwald & Fox, eds.), 2013. For the two states of the title, see: Cohen, ‘The case of the missing author: the title page of Newton’s Opticks (1704), with notes on the title page of Huygens’s Traité de la Lumière,’ pp. 15-45 in: Isaac Newton’s Natural Philosophy (Buchwald & Cohen, eds.), 2001. For a very thorough account of the composition, content, and reception of the Opticks, see: Hall, All was Light: An Introduction to Newton’s Opticks, 1993. We are indebted to Scott Mandelbrote of Peterhouse, Cambridge, for much of the information in our description relating to the provenance of Fatio’s copy of the Opticks, and for information on other presentation copies. Mandelobrote is a staff member of The Newton Project, and is the author of Footprints of the Lion: Isaac Newton at Work (Cambridge: Cambridge University Library, 2001), which accompanied a major exhibition of Newton’s work at Cambridge University Library, as well as other books and scholarly journal articles relating to Isaac Newton.
4to (242 x 193 mm), pp. [iv], 144; 1-137, [1, blank], 138, [1, blank], 139-162, [1], [1, blank], 165-211, [1, errata] (p. 120 of part 2 misnumbered 112), title printed in red and black, 19 folding engraved plates, woodcut diagrams and letterpress tables in the text (paper flaw to part 1 p. 98 with some distortion to 2 lines of text and letters supplied in ink by the printer, a.
Item #5080
Price: $825,000.00