Rabdologiae seu numerationis per virgulas libni duo.
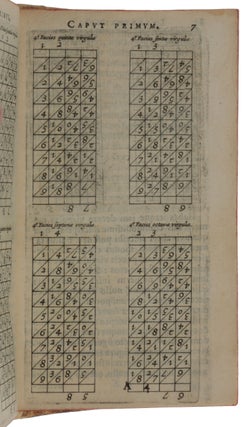
Edinburgh: Andrew Hart, 1617. First edition, very rare, of one of the earliest mechanical calculating devices, using little rods of wood or ivory now known as ‘Napier’s bones’. Napier is best known today for his invention of logarithms, published in 1614 as Mirifici logarithmorum canonis decsriptio, the most important aid to calculation before the advent of mechanical and electronic calculators in the twentieth century. “In 1617 Napier’s intense concern for the practicalities of computation led him to publish another book, the Rabdologiae, which contains a number of elementary calculating devices, including the rods known as ‘Napier’s bones.’ These rods, which in essence constitute a mechanical multiplication table, had a considerable vogue for many years after his death. Each rod is engraved with a table of multiples of a particular digit, the tens and units being separated by an oblique stroke. To obtain the product 267 × 8, the rods 2, 6, 7 are assembled and the result is read off from the entries in the eighth row; thus gives 2,136. Book II is a practical treatment of mensuration formulas. Book III, the method of the promptuary, deals with a more complicated system of multiplication by engraved rods and strips, which has been called the first attempt at the invention of a calculating machine. The concluding section deals with a mechanical method of multiplication that was based on an ‘areal abacus’ consisting of a checkerboard with counters, in which numbers were expressed in the binary scale” (DSB). In this last section, Napier was one of the first to use the decimal point – according to Goldstine (The Computer from Pascal to Von Neumann, p. 4), he “was perhaps the first man to understand, in his Rabdologia in 1617, the use of the decimal point in arithmetical operations” (Goldstine, p. 4). The name ‘Napier’s bones’ appears to have originated from the title of a work by William Leybourn published in 1667 entitled The art of numbering by speaking rods: vulgarly termed Napier’s bones. Leybourn’s use of the term 'speaking rods’ was a mistranslation of the title of Napier’s Rabdologia – this comes from the Greek ‘rabdos’ meaning a ‘rod’ and ‘logia’ meaning ‘collection’, and not, as Leybourn thought, ‘logos’ meaning 'word’. “John Napier, Baron of Merchiston, was born in 1550 just as the Scottish Reformation was starting. He is best known for his invention of logarithms, but he spent a large part of his life devising various other schemes, both mechanical devices and logistical practices, for easing the labor involved in doing arithmetic. He undoubtedly used these devices in the calculation of his first table of logarithms. The best known of these devices is his Rabdologia, or as they are more commonly known, Napier’s rods or Napier’s bones. The name bones arose from the fact that the better quality sets were constructed from horn, bone, or ivory. Various authors have preferred to call them numbering rods, multiplying rulers, or even speaking rods, but the name bones has lasted. Today the bones are considered a mere curiosity while his other two devices have been almost entirely forgotten. The Promptuary of Multiplication was simply a modified version of his bones that, at the expense of being more difficult to construct, eliminated some of the problems of multiplying one multi-digit number by another. It was an interesting idea but never became popular. The local arithmetic device was simply a standard chess or checkerboard used as a modification of the table abacus. Each row and column represented a power of two higher than the one below or to the right. Again, it was never really used by the public because of the seemingly unnatural use of binary numbers. Napier did not at first consider these inventions worthy of publication; however, several friends, particularly Alexander Seton, the Earl of Dunfermline and High Chancellor of Scotland, pressed him to write them up, if only to avoid having others claiming them as their own. His descriptions appeared in a small book entitled Rabdologia in the year of his death and three years after the publication of his description of logarithms. “The idea for the bones undoubtedly came from the gelosia method of doing multiplication. This ancient method probably originated in India and spread to Arab, Persian and Chinese societies by the late Middle Ages. The method was introduced sometime in the fourteenth century into Italy, where it obtained its name from its similarity to a form of Italian window grating. “The method consists of writing down a matrix like grid, placing one digit of the multiplicand at the head of each column and one digit of the multiplier beside each row; the product of each row and column digit was then entered in the appropriate box of the matrix—the tens digit above the diagonal and the units digit below. The final product was obtained by starting in the lower right-hand corner and adding up the digits in each diagonal, with any carry digits being considered as part of the next diagonal … “Napier’s bones are simply a collection of strips of all possible columns of this gelosia table. To perform the multiplication of 456 by 128, one would simply select the strips headed 4, 5 and 6; place them side by side and read off the partial products of 456 times 1, 456 times 2, 456 times 8 (by adding up the digits in each parallelogram to obtain each digit of the partial product); then add together the partial products. Division was aided by the bones in that multiples of the divisor could be easily determined and thus save the time that would normally be spent in trial multiplication … “The obvious disadvantage of the bones was that the user had to write down and add up all the partial products of the multiplicand. In an appendix to Rabdologia, Napier described another, more sophisticated device he called a Multiplicationis Promptuarium. This consisted of a larger set of strips operating on the same principle as the bones, that would eliminate the need for recording and later adding up the partial products. This device never became popular, probably because of the difficulty and expense of constructing the many different strips required for a full set. There is only one known example of the device that predates 1900, a lovely ivory set currently housed in a Spanish museum. The one or two sets that were made in the twentieth century appear to have been constructed only for demonstration purposes” (Tomash & Williams, pp. 1451-3). Napier’s promptuary has been called the first attempt at the invention of a calculating machine (Hawkins, ‘The first calculating machine (John Napier, 1617),’ IEEE Annals of the History of Computing, January 1988). “The third and final section of the Rabdologia is a 37-page addendum that describes what Napier called ‘Location Arithmetic as Performed on a Chessboard’, and this arithmetic is the focus of the present article. Napier's enthusiasm for his Chessboard Calculator is apparent from his remarks in the preface to the addendum, which is worth quoting in its entirety: ‘While working in my spare time on these short methods and seeking ways in which the tedium of calculation might be removed, I developed (not only my logarithms, my Rabdology, my Promptuary for multiplication and other things, but also) a method of arithmetic on a flat surface. As this performs all the more difficult operations of common arithmetic on a chessboard, it might well be described as more of a lark than a labor, for it carries out addition, subtraction, multiplication, division, and [even] the extraction of roots purely by moving counters from place to place. There is one small difficulty in working with it, and that is that the numbers it uses differ from ordinary numbers, so that one must begin by expressing ordinary numbers in the new form and end by reducing them to common form. Either process is simple enough even during the course of the calculation, and overall my method is easier and more accurate than almost any other short method of Arithmetic. I therefore resolved not to bury it in silence nor (as it is so short) to publish it on its own but to subjoin it to my Rabdology after the aforementioned promptuary for the benefit of the studious and the scrutiny of the learned.’ “Despite Napier's enthusiasm, the Chessboard Calculator never seems to have found favor. ‘Location Arithmetic as Performed on a Chessboard’ was largely ignored and in subsequent years was reported on as a mere curiosity. It is somewhat ironic that within Napier’s unheralded Chessboard Calculator lies buried one of the earliest applications of the binary number system—described as ‘a pioneering explanation of binary arithmetic as a computational aid’ by Robin Rider in the Introduction to a translation of Napier’s Rabdologiae (Napier 1990, p. xxiii). We find Napier’s invention to be worthy of explication for at least two reasons: first, his early use of binary arithmetic, which he identified as the ‘one small difficulty in working with’ his Chessboard Calculator, and, second, its potential as a source of enriching educational experiences for today’s students” (Kolpas & Tomash, ‘Napier's Binary Chessboard Calculator – Napier’s Rabdologiae,’ Convergence, December 2018). “Napier’s rods rapidly became popular in England. According to one Seth Partridge, a London-based surveyor and mathematical practitioner, these reckoning rods were easy to make in any material whatsoever; they could either be manufactured by oneself or bought in the London instrument shops: ‘These speaking-Rods may be made either of Silver, Brasse, Ivorie, or Wood, as the maker and user of them best pleaseth, but they are most ordinarily made of good sollid Box, and being thereof made, they are as usefull as those made of any other substance whatsoever, Nay, I hold them more light and nimble then those made of Mettall; …Every practitioner may make them himselfe by cutting the faces of every one of the printed papers of the Rods, and so placed on a square piece of wood as before; or else they are ready made in Wood, by Master John Thompson…’ “In the next centuries a lot of inventors tried to improve and facilitate the work with Napier’s rods, starting with the above mentioned Wilhelm Schickard in early 1620s. In early 1650s, an attempt to make a tool with Napier's rods made the French physicist, cartographer, and engineer Pierre Petit (1594-1677), a King’s Counsellor and Intendant des Fortifications. Petit placed paper strips with Napier’s rods and made a mechanism, the so-called Arithmetical Cylinder or Tambour de Petit (Cylinder of Petit), allowing the paper strips to be moved along the axes. The device he described in his book Dissertations academiques sur la nature du froid et du chaud. Avec un Discourssur la construction & l'usage d'un Cylindre Arithmetique, inventé par le mesme Autheur (Paris, 1653) …
12mo (134 x 79 mm), pp. [xii], 154, with four folding engraved tables at pp. 101, 105, 106 (lettered A-C) and 130, engraved and woodcut illustrations in text. Contemporary blindstamped pigskin (rebacked, preserving original spine). Provenance: Dom-Gymnasium, Merseburg (library blindstamp on title).
Item #5172
Price: $75,000.00