Mechanica: sive de motu, tractatus geometricus. Pars prima. In qua, De motu generalia. De gravium descensu, & motuum declivitate. De libra (Pars secunda. In qua, De centro gravitates. Ejusque calculo; Pars tertia...
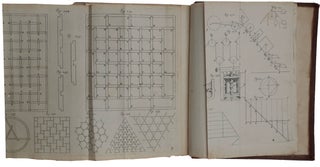
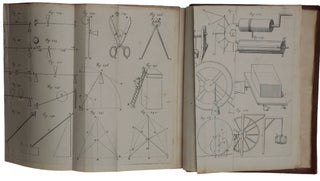
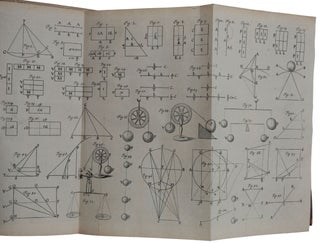
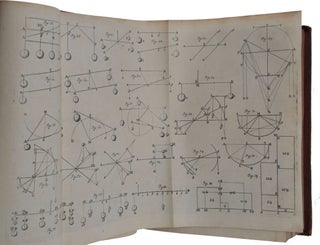
London: William Godbid for Moses Pitt, [1669-] 1671. First edition, very rare when complete with the portrait and all three parts, of this classic treatise on mechanics by Newton’s most important English precursor. It treats both statics (the balance, the lever, centres of gravity, elasticity, and hydrostatics) and dynamics (including the motion of bodies under gravity, and the first comprehensive treatment of the collision of both hard and elastic bodies). “On these investigations, according to Professor Mach, Sir Isaac Newton based his researches contained in the Principia” (Sotheran 5188). All three of ‘Newton’s’ laws of motion are stated in the Machanica, almost two decades before the publication of the Principia. “The first part deals with various forms of motion in a strictly ‘geometrical’, that is, Euclidean, manner, starting with definitions followed by propositions. The motion of bodies under the action of gravity is covered in particular. The final chapter of the first part is devoted to a treatment of the balance and introduces the idea of moment, which is essential for the inquiries into the centers of gravity. In the third part, Wallis returns not only to ancient tradition, but above all to a thorough treatment of the problems of percussion. In 1668 percussion and impact were a major topic of discussion at the Royal Society, and Wallis, Wren, and Huygens submitted papers. In the Mechanica, Wallis extended his investigations, studying the behavior of both elastic and inelastic bodies. Although in style and subject matter it is not a uniform book, at the time it was certainly one of the most important and comprehensive in its field. It represents a major advance in the mathematization of mechanics” (DSB). Wallis is best known for his epoch-making Arithmetica infinitorum (1656), which introduced new infinitesimal methods into geometry; these methods are used and extended in the second and longest part of the Mechanica, which is devoted to centres of gravity. “It is an unmistakable sign of Wallis’s greatness that, unlike most of his predecessors and his contemporaries, his mathematical investigations were not restricted to the field of pure mathematics … of all the contributions which this versatile genius made to the progress of science, few perhaps ought to rank higher than his vast and unwearied researches in mechanics” (Scott, p. 91). “The publication of this monumental work revived interest in mechanics. From being the most neglected of the sciences, mechanics rapidly became not only one of the most powerful, but also one of the most intensely cultivated. This sudden accession to popularity was, of course, in large measure due to Newton, but there can be no doubt that just as Newton owed much in his mathematical researches to Wallis, his obligations in mechanics were not less pronounced” (ibid., p. 126). The Norman copy is the only complete copy listed on ABPC/RBH in the last half-century (Christie’s New York, June 11, 1998, lot 845, $9,660). The Kenney copy realized $912 in 1968. Although reasonably well represented in institutional collections, Wing gives no indication of the completeness of the copies recorded, nor indicates that the work was published in three parts, giving the date, 1670, of the first two parts only. Provenance: George Augustus Shuckburgh, 6th Baronet (1751-1804) (armorial bookplate on front paste-down). Sir George Shuckburgh was a mathematician and Fellow of the Royal Society, who owned a substantial library which included a Gutenberg Bible and other early scientific books. “Wallis indicated his general plan in the Dedication to Part I, which preceded by nearly two years the complete work. Addressing Lord Brouncker the author declared: ‘You have now the First Part, which contains the fundamentals of the whole treatise, and particularly the Doctrine of the Balance. Soon after will follow the Second Part, which deals with Centres of Gravity and the calculation thereof in most curvilinear figures and the solids and the curved surfaces arising from these’” (ibid., p. 107). Modeling his work on Euclid’s Elements, Wallis begins with a series of definitions. “Wallis appears to have been the first to realize the futility of discussing mechanical questions so long as the terms used had no definite and permanent meaning … Force is defined as that which is capable of causing motion, a definition not unlike that afterwards employed by Newton … Wallis, when he speaks of Force in dynamical problems, almost invariable means what we would call Momentum, i.e., the product of mass and velocity … Wallis used Momentum where we should Force, as in … Proposition 11, where he states: ‘if the momentum exceeds the resistance motion results’ … In Chapter III, when he discusses statical problems, he uses the same word Momentum for the product of force into distance, i.e., the modern Moment of a Force about a Given Point … Gravity is defined (Definition 12) merely as Force Downwards; its measure is Pondus (Def. 13) … Wallis was well aware that the ideas concerning weight were in a very confused state, and he tried to disentangle them. He had only the vaguest notion of the difference between Mass and Weight, and he used the word Pondus almost indiscriminately for both … “In Proposition 11, the first Law of Motion, the truth of which had often been implied, appears in a dress only slightly different from that in which it appeared nearly twenty years later [in Newton’s Principia]: ‘If the force is greater than the resistance, motion will result. If there was none before, motion will begin; if it already existed, it will be increased. If the resisting force is greater, it will oppose the motion if there was any, or at least check it. If the two are equal, motion will be neither started nor stopped, and the initial state of the body, either of rest or of motion, will persist.’ In Proposition 12 almost the same statement occurs except that Force is substituted for Momentum … although Wallis was hazy regarding the true conception of Force, and although he seemed to use the terms Force, Momentum, Impetus indiscriminately, he had really grasped their interrelation; for in Propositions 17 to 21 he explains that the momenta of forces are proportional to the forces and to the times during which they act … his Momentum is our Impulse, and his Force our Momentum [so] Wallis’s statement becomes almost identical with the Second Law of Motion, namely, that the Momentum produced is proportional to the Impulse of the Force … Wallis realized the proportionality between the force and the motion produced by it; indeed, he seems to have been thoroughly familiar with the notion many years before it was given such definiteness by Newton in 1687. “Having established the above general principles, Wallis opens up in Chapter II an investigation into the subject of the motion of bodies under the action of gravity. This begins with the Proposition: ‘Heavy bodies, other things being equal, gravitate in proportion to their weights’ … In Proposition 5, there appears a familiarity with the conception of Energy … the ‘force’ of a falling body is proportional to the product of the mass and the distance through which it falls [i.e., its potential energy in our terms]. Further, he realized that this principle was at the basis of such machines as the Inclined Plane etc. … “Chapter III, De Libra (The Balance), deals with the first of the mechanical machines … The fundamental principle is enunciated in Proposition 12 – the weights act in the ratio of their magnitudes and their distances from the centre of motion combined, and the equality of this ratio must persist for equilibrium, even if the beam of the balance be not horizontal … For what we call the Moment of a Force about a given point Wallis introduced the word Ponderatio, a word certainly more suggestive of the idea underlying it than our Moment. Lagrange, it may be noted [in his Mécanique analitique (1788), p. 9], was of the opinion that Wallis was one of the few who had really grasped the idea of Moment … This Ponderatio is the product of the force into the distance … The latter part of the chapter is taken up with the investigation of the conditions of equilibrium of a beam loaded at different points … “Wallis’s demonstrations were immeasurably more exhaustive and thorough than anything which had gone before. It was essential that they should be, for this investigation on the Principle of Moments and its application was the prelude to a much more important piece of research, namely, an investigation into the methods of determining the Centre of Gravity of different figures … This enquiry begins in Chapter IV, De Centro Gravitatis. On the threshold are recounted the familiar properties of the Centre of Gravity which had already been elaborated by Galileo and Stevin, namely, a body supported at its Centre of Gravity is in equilibrium; there is only one Centre of Gravity, and this lies on any axis of equilibrium; the Centre of Gravity of two bodies joined together is on the line joining the two Centres of Gravity. “Wallis’s method of finding the Centre of Gravity is based upon three principles: “Now, if a body be divided into a large number of small parts, not necessarily equal but at least increasing or decreasing according to some known law, their total sum may be ascertained by the methods already elaborated in the Arithmetica infinitorum … apart from a persistent haziness concerning Infinity, the work is not materially different from a modern treatise … “The investigation is directed to all kinds of figures. In Proposition 14 curved figures are introduced, and these are followed by solids of revolution. At Proposition 20 the cycloid is introduced. He investigates many of the properties of this curve, and he shows that its length is four times that of the axis. This rectification had, of course, been accomplished a dozen years earlier [by Pascal], but Wallis broke new ground by examining many of its properties, by finding the lengths of different portions of the curve, and by determining its centre of gravity … After this interlude, Wallis passes to the spiral, the cissoid, and the conchoid, each of which is treated with a thoroughness hitherto unknown in the history of the subject … “The third part of the Mechanica deals with the Balance and with the machines for facilitating work. There is also a chapter on the Composition of Motions …, another on Hydrostatics and the Pressure of the Air, and a concluding chapter, Variisque Quaestionibus Mechanicis. But probably the most original and at the same time the most stimulating chapters were De Percussione and De Elatere et Resilitione seu Reflexione, where problems on percussion are investigated with marked thoroughness. Without doubt this part of the work had a pronounced influence upon the course of mechanical learning during the next fifty years or more … “The Royal Society, in 1668, initiated an investigation into the laws relating to the collision of bodies, and this proved a great stimulus to the more mathematically minded of the scholars of the period. In response to this invitation three geometers attempted an elucidation of the problems raised, and each communicated his results to the Society – Wallis on November 15, 1668, Wren on December 17, and Huygens, who was abroad at the time, submitted his observations early in the next year … [In the chapter De percussione, Wallis] extends his investigation, dealing first with bodies inelastic and then with bodies elastic. “If a perfectly hard body impinge upon another, the subsequent motion of each is governed by their respective momenta before impact. Basing his investigation upon the Principle [of Conservation] of Momentum, he shows how to find the common speed after impact … In these observations, Wallis was beginning to approach the Third Law of Motion in its most generalized form, namely, that … momentum is as much diminished in a striking body by the resistance it experiences as it is increased in a body struck by the impact, and the quantity of motion remains unaltered … “In his next Proposition, Wallis enunciates a theorem in which the idea underling Newton’s Second Law of Motion is even more clearly discernable. The total effect of a force in producing change of momentum is called its Impulse; for this Wallis uses the expression ‘magnitudo Ictus’ – the magnitude of the blow – and Proposition 5 states that the magnitude of the blow is double the momentum lost by the striking body – that is to say, it is equal to the total change of Momentum – the Momentum lost by the one plus the Momentum gained by the other … “In Proposition 15 he introduces the notion of Centre of Percussion, or as he calls it Centre of Forces” (ibid.) “If a body rotates about an axis and its motion be suddenly checked by the retention of one of its points, the force of the percussion will vary with the position (the distance from the axis) of the point arrested. The point at which the intensity of the impact is greatest is called by Wallis the centre of percussion” (Mach, p. 327). “But here he makes a slip, which every one of his predecessors and contemporaries made, with the sole exception of Huygens, in that he regarded the Centre of Percussion and the Centre of Oscillation as identical … This conflict of opinions was revived when Huygens’ monumental work [Horologium oscillatorium] appeared in 1673 … “In Chapter XIII, De Elatere, & Resilitione seu Reflexione, Wallis attacks the more formidable problem of Impact of Elastic Bodies … [His conclusions] may be summarized in modern language and notation thus: When two bodies impinge the sum of their momenta along the line of impact is the same as before, and (for bodies perfectly elastic) the relative velocity after Impact is the same as that before Impact, though reversed in direction … This was a notable advance upon anything that had gone before, and, save in two respects, was quite equal to what was subsequently delivered by Newton. In the first place, Newton’s notation was much more concise, and more readily understandable. Secondly, Newton introduced the coefficient of restitution [enabling him to deal with bodies that were only partially elastic], and thus carried Wallis’s investigation to its consummation … “[In Chapter X, De motibus compositis, acceleratis, retardatis, & projectorum,] his first proposition gives greater precision to a principle with which Galileo had startled the scientific world, namely, that a constantly applied force produces not simple a velocity but a change of velocity, i.e., an acceleration … Furthermore, if this force is uniform the acceleration produced will also be uniform … This he demonstrates graphically, and though his investigation lacks the definiteness of Newton’s Second Law, there is in Wallis’s work something more than the germ of Newton’s. “Now gravity is a constant force; therefore, if we exclude the resistance of the air, a body falling under the action of gravity will be uniformly accelerated … if a body, instead of falling vertically, rolls down an inclined plane, it will acquire the same velocity as if it had fallen through the same height vertically. “Proposition 6 contains the important principle of the Parallelogram of Velocities – if upon a body free to move there be impressed two velocities which can be represented in magnitude and direction by the angular sides of a parallelogram, the diagonal through that angular point will represent its acquired velocity in magnitude and direction … This is extended in Proposition 7: If a uniform motion is compounded with an accelerated motion, the motion will deviate from a straight line, and in the case of a body projected at an angle the path described by the body will be a parabola. Of course, all this had been enunciated by Galileo; Wallis’s investigation, however, is very much more comprehensive, for, as usual, he generalizes his results, and considers the motion compounded of all kinds of motions, e.g., if a uniform speed be compounded with one which is accelerated in the duplicate ratio of the times, so that the displacement is in the triplicate ratio of the times, the path will be a cubical parabola” (ibid.). Chapter XIV, De hydrostaticis, & aeris aequipondio, has been little studied by historians. “In the second half of the 1650s, after news of the invention of the air-pump by Guericke (1654) reached England, Boyle, Hooke, and others improved the pump and set out experimentally to investigate the properties of the vacuum and the ‘spring’ of the air. Boyle first published their results in New experiments physic-mechanical, touching the spring of the air and its effects (1660), followed by other tracts in 1663 and 1666. Perhaps less well known is that in 1671 John Wallis published within his Mechanica a hydrostatical treatise that included pretty much the main physical conclusions reached in Boyle’s and Hooke’s experiments but recast and articulated in mathematical argument. In effect what Wallis achieved was to turn hydrostatics and pneumatics into a mixed mathematical science in the style of Archimedes and Stevin” (Roux, pp. 160-161). Carl B. Boyer, in his article ‘History of the Derivative and Integral of the Sine’ (The Mathematics Teacher 40 (1947), 267-275) noted that Wallis’s Mechanica made an important contribution to the history of trigonometry, recognizing the periodicity of trigonometric functions. According to Boyer, “a portion of the sine curve appears for the first time in history” about 1635 in an article by Gilles de Roberval, a French mathematician who experimented with pre-calculus techniques in curve analysis. However, Roberval provided an illustration only of the first quarter of a complete sine curve. For a while, this was known as ‘Roberval’s curve.’ Boyer, noted, however, that “the first clear-cut recognition of trigonometric periodicities seems to be that of Wallis in his Mechanica of 1670. Here two full cycles of the sine curve are clearly drawn; and the periodicity is evidenced by an accompanying statement that the sine curve increases throughout the first, fourth, eighth, ninth quadrants, and so forth.” The sine curve is labelled as fig. 201 in Mechanica, and is referenced on pages 504 and 505. Wing W-593; Norman 2181. Mach, The Science of Mechanics, 1919. Roux, The Mechanization of Natural Philosophy, 2012. Scott, The Mathematical Work of John Wallis, 1938.
4to (199 x 154mm.), pp. [6], 1-109, [4], 109-569, [3], 571-771, [1], with portrait frontispiece of Wallis drawn and engraved by William Fairthorne (1616-91) and 17 folding engraved plates. Contemporary (or slightly later) panelled calf (joints cracked but holding, minor rubbing).
Item #5201
Price: $32,500.00