Plain Astronomy. Manuscript volume of notes on practical astronomy and mathematics.
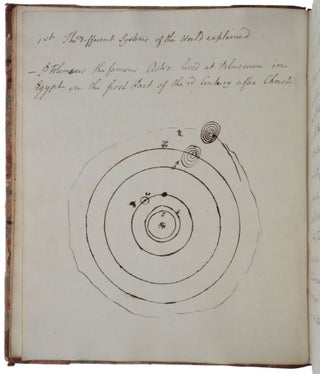
[N.p. N.p., ca. 1780]. A fascinating manual of astronomy, particularly as it relates to the form of the motions of the heavens, dating from the period 1780-1825, probably from the beginning of that range. It is in a single hand (with the exception of one page), though with some variations indicating that different parts of the MS were written at different times. The MS could have been prepared for personal use or as part of public tuition (probably the former). The writer summarizes the subject matter of the manual on the first leaf: ‘Astronomy is that part of Natural Philosophy which treats of the Phenomena of the heavenly Bodies. It is divided into 2 Parts, Physical and Plain: by the latter we discover their Motions from the Apparent Motions; by the former the Causes of these real Motions.’ The MS is in three parts, which are distinct in terms of subject matter. The first part covers the motion of the Earth around the Sun, and its rotation about its axis, with the consequences for the apparent motions of the Sun and the heavens; with the Moon and its phases and motion; and with lunar and solar eclipses. There are several references to John Keill’s An Introduction to the True Astronomy (London, 1721 and subsequent editions). The second part principally consists of a discussion of section 11 of Newton’s Principia (1713 or later editions), in particular as it relates to the motion of the moon. This part ends with a short section on algebra, particularly polynomials, which seems to have been composed more haphazardly than the remainder of the text. The third part, which runs backwards starting from the end of the notebook, gives demonstrations of various results in Book I of Principia, notably the theorem that the orbits of the bodies in the solar system do not precess if and only if the central attractive force operating on them is exactly inverse-square. This is an important result not only for Newton’s system of universal gravitation but also for the observational astronomy of the solar system which is discussed in the opening section of the book. Between the end of the second part and that of the third there are a few blank leaves, and others have been torn out, but the text appears complete. The MS appears to be a working through of at least two different texts, beginning with Keill’s on astronomy. The first part of the MS refers particularly to the material in chapters 7-14 of Keill. It begins with the geometry of the sphere of the Earth and its orbit, great circles and poles, the plane of the ecliptic, equinoctial points, and the Tropics of Cancer and Capricorn. Then comes a section on the different systems of the world, Ptolemaic, Tychonic, and Copernican, illustrated by a diagram. The arguments supporting each system are given, including the aberration of the fixed stars, discovered by James Bradley in 1729, which supports Copernicus. It is noted that the Sun’s apparent diameter varies according to the time of year, which is explained by the fact that the Earth’s distance from the Sun is not constant. Kepler’s laws are stated, with a long discussion of the area law, and a statement that the Earth’s orbit is an ellipse. The consequences of the fact that the plane of the Earth’s orbit is inclined at an angle to the plane of the ecliptic are discussed (the seasons). There is a section devoted to the precession of the equinoxes – the author notes that “Sir Isaac Newton has demonstrated that it arises from the broad spheroidal figure of the Earth.” The author then turns to sunspots and the arguments for and against their being on the surface of the Sun. Then comes a long discussion of the planets: the planes and periods of their orbits, phases, conjunctions, retrograde motions, apparent brightness, and their distances from the Sun. Special attention is given to the phases of Venus, the varying appearances of Mars, and Saturn’s rings. This is followed by an extensive discussion of the Moon: its phases and motion, and the fact that the same face is always turned to the Earth (which implies that the Moon turns on its axis in the same time as it takes to orbit the Earth). This first part concludes with a fairly detailed account of lunar and solar eclipses. The second and third parts are notably more mathematical in nature than the first. The second works through Section 11, Prop. 66 of Principia and its corollaries, which presents the perturbations of a remote body on a two-body system (such as the Sun on the Earth-Moon system). This is one of the most difficult parts of Principia, and one with which Newton was never completely happy (and which is not entirely correct). The language used by the author of the notebook is reminiscent of the Principia but is primarily directed at following through Newton’s working. There is a reference to a numbered figure ‘80’ which does not appear to be numbered in any edition of the Principia. But it seems likely that the language and form of this discussion derives from familiarity with Robert Thorp’s edition of Book 1 of the Principia (1777; cf. the notes published in Latin in 1765: pp. 266-90 in 1777), although Thorp is not referenced explicitly (as Keill is). Thorp does have a figure 80 but it is not clear that he is the author being used at that particular point. There is then a discussion of algebra and the solution of equations which is fragmentary and incomplete, followed by a number of blank and torn-out pages. The third part of the manuscript consists of a reading of various sections of Newton’s Principia (1713 or later editions). Again, it appears to take the form of working through and in some cases repeating the proofs of Newton’s work, rather than representing a translation or paraphrase. It is not based on Motte’s translation nor does it correspond with the partial translation and edition of Thorp. It does not appear to be based on any other intermediary between Newton and the writer (e.g. Pemberton) but to rely on Newton’s Latin original, here rendered in places pretty exactly into English. It renders propositions 43 to 59 of section 9 of book 1 of the Principia, which concern the motion of bodies in moveable orbits and the motion of the apsides. This is a topic which is still of some considerable interest to astronomers and historians of astronomy. Here Newton introduces what has come to be called Newton’s ‘rotating ellipse proposition,’ in which a rotating (or precessing) ellipse is described by a body, for which the central force includes a term proportional to the cube of the distance from the focus; this rotating ellipse is compared with a similar stationary ellipse in which another similar body rotates about the same centre of force. Careful analysis leads to expressions for the extra inverse cube force, depending on the number of upper and lower apses found in the moving ellipse. This part of the notebook includes the demonstration of the important proposition that the extra inverse cube force is absent, i.e., the central force is exactly inverse-square, if and only if the orbits of the bodies in the solar system do not precess. From the hand (which seems constant throughout the book, although with some considerable variation which might indicate a second writer or more likely the same writer at a different time or with a different pen), and the paper, we can with some confidence date the notebook to the period 1750-1825. If our supposition that it was Thorp’s edition of Principia which was being used, we might be able to narrow its date down to 1780-1825. The section of the planets in the first part does not mention Uranus (Georgium sidus), discovered by William Herschel in 1781, which appears to place this as an upper bound. This would therefore suggest a composition date in the late 1770s. We are indebted to Scott Mandelbrote for his assistance with the description of this notebook.
4to (196 x 162 mm), manuscript in ink on Dutch paper with Maid of Dort watermark without countermark. 101 and 26 leaves of text and diagrams, 39 blank leaves in the middle, last 26 leaves reversed, illustrated with several astronomical and mathematical diagrams, including one of a solar system. Late 18th century half calf, marbled sides.
Item #5309
Price: $5,000.00