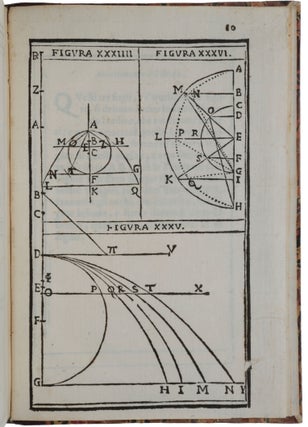
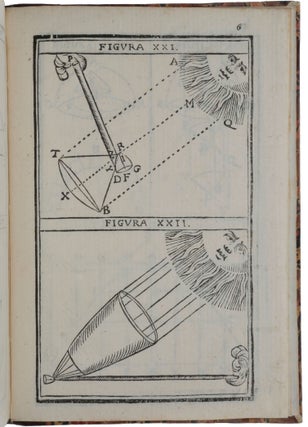
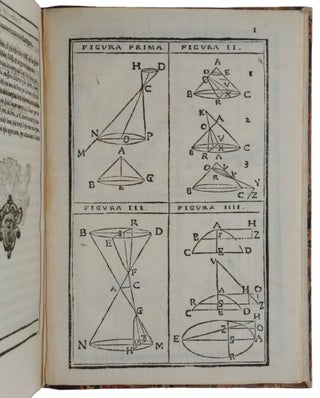
Lo Specchio Ustorio overo trattato delle settioni coniche, el alcuni loro mirabili effetti intorno al lume, caldo, freddo, suono, e moto ancora...
Bologna: Clemente Ferroni, 1632. First edition, rare, of Cavalieri’s highly important treatise on conic sections and their applications in optics, acoustics and, perhaps most significantly, mechanics. Its importance in the history of the telescope is well-known: “Cavalieri’s design may well have been in all the essentials a direct anticipation of Newton’s reflecting telescope. Clearer and stronger, however, is the claim that Cavalieri anticipated the Cassegrainian telescope” (Ariotti, p. 316). But the importance of Specchio in the history of mechanics may be greater, as it was in the chapters (38-40) of this work devoted to motion that Cavalieri first published the discovery that the path traversed by a projectile moving under gravity is a parabola. Although this was certainly known to Galileo (and to Thomas Harriot) at the time (and Cavalieri credits Galileo with the discovery), Galileo did not publish it himself for another six years, in the Discorsi (and Harriot never published it). “Galileo’s Dialogo was not the only work to anticipate some of the results later presented in the Discorsi. In that same year Cavalieri published Lo specchio ustorio, in which he devoted two chapters to falling bodies and parabolic trajectories relying on his new mathematics. Cavalieri was readying for publication Geometria indivisibilibus (1635), his mathematical masterpiece on the method that dominated mid-century infinitesimal mathematics. Cavalieri attributed to Galileo his main results on motion, such as the odd-number rule and parabolic trajectories. As to the latter, he stated that, neglecting gravity, the trajectory of a body shot at any angle would be rectilinear, and he tried to prove the relation [distance fallen under gravity is proportional to time2, from which the parabolic nature of the trajectory is a straightforward deduction] with his indivisibles” (Meli, p. 91). “In this work, we find a theory of conics with applications to optics and acoustics. Among the former, we note the idea of the reflecting telescope, of which – according to Piola and Favaro – Cavalieri was the first inventor, preceding Gregory and Newton; determination of the focal length of a lens of uneven sphericity; and explications of the burning glass of Archimedes. In the field of acoustics, Cavalieri attempted the archaeological reconstruction of the resonant vases mentioned by Vitruvius and used in theaters for amplifying sound” (DSB). In the optical chapters, Cavalieri refers frequently to Kepler’s Dioptrice (1611). Cavalieri (1598-1647) was an outstanding mathematician, and a friend and disciple of Galileo, although the publication of the present work caused a temporary rift between them – Galileo believed that Cavalieri had published some of his [Galileo’s] own results on projectile motion, then still in manuscript, without permission. The dispute was resolved, and in the Discorsi Galileo praised the Specchio for its treatment of optics and lauded Cavalieri as a new Archimedes.. ABPC/RBH lists three copies since the Norman copy (which realized $11,500 at Christie’s in 1998). “Bonaventura Cavalieri, celebrated for his method of indivisibles, was influential in preparing the ground for the integral calculus of Newton and Leibniz. Like a number of disciples of Galileo, Cavalieri was a man of the cloth. Born in Milan around 1598, by 1616 he was in Pisa studying under the first disciple of Galileo, Benedetto Castelli, whom he later replaced in teaching mathematics. In 1629 Cavalieri was appointed to the chair of mathematics at Bologna, where he died in 1647 … In [Lo specchio ustorio] Cavalieri concerned himself with reflecting mirrors for the express purpose of resolving the age-long dispute of how Archimedes allegedly burned the Roman fleet that was besieging Syracuse in 212 BC. The book, however, goes well beyond the stated purpose and systematically treats the properties of conic sections, reflection of light, sound, heat (and cold!), kinematic and dynamic problems, and the idea of the reflecting telescope. “Past masters such as Witelo, Roger Bacon, Orontius, Cardano, della Porta, Grienberg, and others have delved into the problem of mirrors, noted Cavalieri, and have taught us much. However, they have not treated the problem systematically nor dealt with mirrors shaped according to every conic section. Such things, Cavalieri stated at the beginning of the Specchio, he would do, or, rather, after a wait of several years he would now make public because of the pleas of somebody whose judgement has always proven sound [this was Cesare Marsili] … “Cavalieri proceeded step-by-step, first with something well-known: the law of reflection of incident light which had been demonstrated by many beginning with Euclid. The angle that an impinging ray of light forms with a flat reflecting surface is equal to the angle of reflection. But, added Cavalieri, this law is valid for any surface provided that by angles of incidence and reflection we understand those formed with the plane tangent to the surface at the point of incidence. After this, ‘We shall accept the above principle not only with respect to light, but also to motion as well as sound – as the Jesuit father Biancano had done in his Echometria – heat, cold and in short for anything the motion of which is in straight lines’” (Ariotti, pp. 307-308). Cavalieri then goes on to state and prove many properties of the parabola, ellipse and hyperbola that will be needed in the remainder of the book. “After more properties and more proofs, Cavalieri concluded his formal treatment of conics with a comprehensive and convenient table of reflecting surfaces and modes of reflections. Appropriately called Tavola specolaria, or Table of Specula, or Mirrors, it shows what reflecting surfaces are required for maintaining or transforming rays which are parallel, convergent or divergent into rays which are convergent, divergent, or parallel. For example, by reading down along the third column and to the left along the first row, it is seen that convergent rays can be made parallel by using a convex parabolic or spherical reflecting surface. Similar operations are explained in the short Chapter 25 that Cavalieri added for the purpose. “Cavalieri then returned to his original problem – the burning mirror – and in so doing he described the basic elements and design of the reflecting telescope … Burning mirrors, Cavalieri noted, can be constructed in combination with lenses: ‘instead of small parabolic mirrors we could use spherical ones, or use lenses because the concave lens does the function of the small convex mirror and the convex lens that of the concave … as we learn from Kepler’s Dioptrice. “After a lengthy discussion on the history of burning mirrors, Cavalieri came directly to the question of reflecting telescopes: ‘I could also say that the effect of the telescope could possibly be obtained from a combination of these mirrors or of mirrors and lenses although the facility of producing the spherical figure will make it so that we will use it rather than the others. Given that the concave mirror does the function of the convex lens, and the convex mirror that of the concave lens, it is also clear that if we combine the concave with the convex mirror or with a concave lens we would have the effect of the telescope and such was perhaps the mirror of Ptolemy.’ “Indeed, Cavalieri had himself considered how such a telescope could be made: ‘On this point, I shall not omit saying that as I heard more than once of the search by some people for a way of combining glasses that would produce the effect of the telescope, I thought that such could be accomplished by placing a concave lens at one side and a small concave mirror at the other. For, if we take these two glasses and interpose a flat mirror which faces us and which can be brought nearer or farther away as is needed to see the image distinctly in the small concave mirror – and we shall see both the one and the other in the flat mirror – the telescopic effect will be achieved’ … “Thus Cavalieri’s design may well have been in all the essentials a direct anticipation of Newton’s reflecting telescope” (Ariotti, pp. 311-316). Newton would have had easy access to the Specchio since there was a copy in the library of his mentor Isaac Barrow. “Clearer and stronger, however, is the claim that Cavalieri anticipated the Cassegrainian telescope, an anticipation which has been entirely overlooked. Perhaps this has gone unnoticed because it occurs in the context of the Specchio’s treatment of the reflection of sound, more specifically in a discussion of what Cavalieri calls the ‘acoustic vases of Vitruvius’, rather than in his chapters on reflection of light. “The design envisioned by Cavalieri consists of two nesting reflecting services the larger of which is perforated at A [Fig. XXIII]. After entering through A and impinging upon the convex surface K, the sound is reflected towards the concave surface OAR, from which it is then reflected through the opening FP to the listeners. Now although the device is clearly an acoustic one, the essential idea is in anticipation of the telescope of Cassegrain. For if in accordance with the principles enunciated by Cavalieri himself at the beginning of the Specchio – the direction of travel is a matter of indifference and in all respects the reflection of light takes place exactly as a reflection of sound, we may regard the concave surface OAR as the perforated main mirror and the convex surface K as the secondary of a Cassegrainian telescope. What is lacking is an ocular, which, given Cavalieri’s awareness of the need for one in reflecting telescopes, he would no doubt have added” (ibid., pp. 316-317). Newton put forward his design for a reflecting telescope in 1668, and Laurent Cassegrain published his design slightly later. Cavalieri makes several important contributions to mechanics in this work. In his Elogio of Cavalieri, Piola (Sparavigna, p. 73) notes that, in the three chapters devoted to motion, when speaking of the composition of motions, Cavalieri wrote of the ‘indifferenza de’ corpi al moto,’ which anticipated the notion of inertia usually credited to Gassendi in his De motu impresso a motore translato (1642) and which later became a central concept of Newtonian mechanics. But the most important contribution of Specchio to mechanics was to publish for the first time the parabolic nature of projectile trajectories. The analogy between optics and the motion of heavy bodies was a recurring them of the time. “Thomas Harriot and Galileo were early seventeenth-century contemporaries in different countries, each searching for new principles of compound, projectile motion. Both were fully aware of the mechanical analysis of reflection within optics as compound, projectile motion – where the trajectory of light is unaffected by gravity due to its lack of weight. Indeed, the notion that projection-impact-rebound phenomena were governed by the law, and dynamics, of reflection was the zeitgeist of the times. Moreover, Harriot had been the first to construct a theory of impact based on the full mechanical generalization of the optical principles he found in such ‘light-mechanical’ analyses – his ‘doctrine of reflexions’ (1619). Perhaps he had also sought to grasp the basics of compound projectile motion under gravity via optical principles of compound, projectile motion? Perhaps Galileo had used his knowledge of optics to inform the conception of new principles of compound, projectile motion too?” (Smith, p. 299). “Galileo, in the last part of his final work Discourses on Two New Sciences (1638), proved that the trajectory of a particle travelling through a non-resisting medium is a parabola. The proof is simple and straightforward once it is known that the vertical distance the object falls from rest is proportional to the square of the time elapsed and that the projectile’s horizontal velocity will remain uniform. As a matter of fact a similar proof had been published six years earlier in a book on conic sections that Bonaventura Cavalieri, a pioneer of the calculus who knew Galileo and who had studied mathematics under one of Galileo’s pupils, Benedetto Castelli. Galileo was indignant when he first learned of Cavalieri’s publication; he wrote to a friend [Cesare Marsili] that the proof was the fruit of studies he had begun 40 years earlier and that the least he deserved was the courtesy of first publication. No one knew better than he, he said, how hard it had been to make the discovery and yet how easy it was to work out the truth when the shape of the trajectory was known. “Cavalieri was much distressed when he learned of Galileo’s wrath and he wrote at once to say that he had credited both Galileo and Castelli in his book, a copy of which he sent to Galileo. He added that everyone knew the discovery was Galileo’s and that he himself had believed Galileo had already published it. Galileo was satisfied and went out of his way in Discourses on Two New Sciences to praise Cavalieri as a new Archimedes. “Some historians of science have naturally wondered how much of this sequence of events could be believed. Was it really possible that a man who had made such a discovery would never have mentioned it in print over a span of three decades? On the other hand, would Cavalieri have said that he had believed the result to have been already published by Galileo if the discovery and not just the proof was really his own? “These questions can now be answered on the basis of Galileo’s notes on motion preserved at the National Central library in Florence in Volume 72 of the Galileian manuscripts. It is certain that Galileo discovered the parabolic trajectory no later than 1608 and proved it mathematically early in 1609, although he did not mention it in print until 30 years later” (Drake & MacLachlan, p. 102). Carli-Favaro 29 (132); Cinti 190 (92); De Caro 63; Honeyman II 642; Norman 418; Riccardi I 323; Ariotti, ‘Bonaventura Cavalieri, Marin Mersenne, and the reflecting telescope,’ Isis 66 (1975), pp. 302-321. Drake & MacLachlan, ‘Galileo’s discovery of the parabolic trajectory,’ Scientific American 232 (1975), pp. 102-111. Meli, Thinking with Objects, 2006. Smith, ‘Shining a light on Harriot and Galileo: On the mechanics of reflection and projectile motion,’ History of Science 53 (2015), pp. 296-319. Sparavigna, Gabrio Piola e il suo Elogio de Bonaventura Cavalieri, 2013.
4to (209 x 147 mm), pp. [xvi], 224, [1, ‘Avvertimento a Librari’] (p. 92 incorrectly numbered 94), with 36 diagrams on 10 leaves of woodcut plates, woodcut device of San Girolamo on verso of title. Eighteenth-century half-calf and marbled boards, spine gilt (a little rubbed).
Item #5314
Price: $13,500.00