De viribus vivis dissertatio.
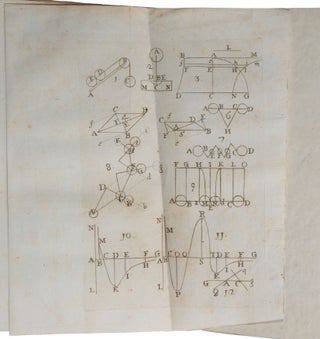
Rome: typis Komarek in via Cursis, 1745. First edition, very rare, of the first published statement of Boscovich’s universal force law, the basis of his atomic theory of matter, which prefigures much of his masterpiece Philosophiae Naturalis Theoria Redacta ad Unicam Legem Virium in Natura Existentium (1758) – at the beginning of part I of the Philosophiae, Boscovich states that he had first developed his theory in 1745 (… Theoria, in quam incidi jam ab Anno 1745). “The ‘Theory of Natural Philosophy’ is now recognized as having exerted a fundamental influence on modern mathematical physics … As the title of his book implies, he considered that a single law was the basis of all natural phenomena and of the properties of matter; that the multiplicity of physical forces was only apparent and due to inadequate mathematical knowledge” (PMM). “In spite of his important contributions to mathematics, astronomy, and optics, today Boscovich is best known for a unified theory of matter based on the hypothesis of point atoms governed by a universal law of force. The basic features of this remarkable theory go back to a treatise of 1745, De viribus vivis” (Kragh, p. 19). This universal force law was inspired partly by Boscovich’s refusal to accept Descartes’ assertion that the velocities of colliding bodies changed discontinuously, and partly by the 31st query with which Newton concluded the fourth edition of Opticks, which proposed that attractive and repulsive forces operate alternately between the particles of matter. Boscovich’s force law is repulsive and tends to infinity at short distances, rendering direct contact between particles impossible, while at longer distances it is alternately attractive and repulsive; this enabled Boscovich to interpret cohesion, impenetrability, extension, and many physical and chemical properties of matter, including its emission of light. Boscovich’s theory “was not only the first general mathematical theory of atomism, but more specifically it was the first scientific theory to treat all the ultimate constituents of matter as identical; to employ finite numbers of point particles; to eliminate Newtonian mass as a primary quantity, substituting a kinematic basis; to postulate a relational basis for the mathematical treatment of inertia and of all space and time observations; to propose to derive all physical effects from a single law; to eliminate the scale-free similarity property of the Newtonian law, introducing natural lengths into continuous laws so as to determine unique equilibrium positions and other scale-fixed properties; to employ a power series to represent an observable” (Whyte). “A natural philosopher, mathematician, physicist, astronomer, geodesist, engineer, and poet, Boscovich was, in the words of the physicist John Henry Poynting, ‘amongst the boldest minds humanity has produced.’ Boscovich published about one hundred books and papers, most of them in Latin … The French astronomer Joseph Jérôme Le Français de Lalande said that in each of these works there are ideas worthy of a man of genius” (Whyte in Encyclopedia of Philosophy). In 1958, Werner Heisenberg wrote: “Boscovich’s work contains numerous ideas that have found their deserved place only in the modern physics of the past 50 years.” ABPC/RBH list only one copy. OCLC records Huntington, Smithsonian, American Philosophical Society, Harvard, Princeton, and Brown (not on COPAC). “The occasion that led Boscovich to the formulation of his dynamic theory of forces was Father Carolus Scherffer’s suggestion of studying the center of oscillation (or center of percussion) of solid bodies. This research led Boscovich to the investigation of the phenomenon of impact or collision of two bodies, a subject dealt with in his De viribus vivis. In sections 16 and 17 of his magnum opus, A theory of natural philosophy, Boscovich writes: ‘In the year 1745, I was putting together my dissertation ‘De Viribus vivis,’ and had derived everything that they who adhere to the idea of Leibniz, and the greater number of those who measure “living forces” by means of velocity only, derive from these “living forces” … I then began to investigate somewhat more carefully that production of velocity which is thought to arise through impulsive action, in which the whole of the velocity is credited with being produced in an instant of time by those who think, because of that, that the force of percussion is infinitely greater than all forces which merely exercise pressure for single instants. It immediately forced itself upon me that, for percussions of this kind, which really induce a finite velocity in an instant of time, laws of their actions must be obtained differently from the rest. “However, when I considered the matter more thoroughly, it struck me that, if we employ a straightforward method of argument, such a mode of action must be withdrawn from Nature, which in every case adheres to one and the same law of forces, and the same mode of action. I came to the conclusion that really immediate impulsive action of one body on another, and immediate percussion, could not be obtained, without the production of a finite velocity taking place in an indivisible instant of time, and this would have to be accomplished without any sudden change or violation of what is called the Law of Continuity; this law indeed I considered as existing in Nature, and this could be shown to be so by a sufficiently valid argument’” (Jammer, p. 171). “In a nutshell, [Boscovich’s] theory prescribes that every process in the world, beginning with those regarding the farthest stars down to those of the smallest particles, is an effect of a unique force that is repulsive at minute distances, attractive at large distances, and alternatively attractive and repulsive at intermediate scales. More exactly, bodies tend to move away from one another (repulsion) at very short distances, with a repulsive force that grows to infinity when the gap dividing them is infinitely small. However, they tend to move toward one another (attraction) when the interval involved is large enough (e.g., at planetary distances), so that it approximates Newton’s gravitational law. Between these two extremes (infinitesimal distances – planetary distances), bodies alternatively approach and move away from one another depending only on the distances at which they are posed. Boscovich argued that, at distances greater than those characterizing the solar system, the force could become repulsive again, so that the stability of the system is ensured. “The idea of the curve [representing the dependence of the force on distance] was first introduced in a 1745 dissertation, De viribus vivis (On the living forces), in order to avoid the abrupt changes of velocity that were prompted, according to Boscovich, by the Cartesian treatment of collision. For Descartes and his devotees, Boscovich contends, velocity changes – hence motions – are generated through collisions. However, he observed that the Cartesian rules of impact allow for an immediate inversion of velocity in the instant of collision [see the illustration of colliding spheres on the plate in De viribus] … if Descartes was right, then the velocities would abruptly be destroyed and immediately re-created at the instant of contact. But this was something that Boscovich was not willing to accept. On the contrary, he proclaimed that instantaneous changes in the state of motion of bodies should be avoided as contrary to nature, for ‘it is already widespread the judgement of many people, that in nature nothing happens by jump’ (Communis iam est multorum sententia, nihil in natura per saltum fieri) [§45 of the present work]. Continuity of natural processes, Boscovich insinuates, must simply be assumed as real. Conversely, there is a version of the Newtonian theory of distant forces that is able to preserve the continuity of processes: there should be a certain mechanism according to which bodies slow down when approaching one another and pass through all velocity degrees before stopping, changing, or inverting their directions. Such a mechanism was explained in terms of a repulsive force (determination) acting at a short distance and growing when the distance lessens” (Guzzardi, pp. xi-xiii). Boscovich’s force law was illustrated on the plate in De viribus “in the form of an elegant diagram that vividly represents the most important features of the theory. These can be described in qualitative terms as follows: The curve expresses a force acting between two points, one at the origins of the axes in A and the other moving along the x-axis. With the distances plotted on the x-axis, the force intensity is represented on the y-axis. It is a continuous quantity that varies with distances: at each distance, there is only one possible force value (or magnitude or degree); if distance is only slightly varied, then force is also varied. In this sense, the force is a continuous function of the distance. Repulsion and attraction are not different forces, but rather different phenomenal manifestations of the same force. Looking at the graph, force is repulsive when the curve is above the x-axis and attractive when it is under it. Moreover, it is infinitely repulsive when the distance is infinitely small, and infinitely small when the distance grows infinitely. In between, the force is alternatively repulsive and attractive, depending on distances, and, because force is conceived as a continuous function of x, there must be distances at which attraction turns into repulsion, and vice versa. “Determining the distances at which force inverts its ‘sign’ or ‘direction’ is a matter of experimental physics: as Boscovich already emphasized in one of his early works, finding the points at which inversions occur (i.e., the points at which the curve cuts the axis) is an empirical problem ‘to be investigated from the phenomena’ (§56) … “By these means, Boscovich maintained, all natural phenomena are described: gravitation on the largest scale; the impenetrability of matter at infinitesimal distances (so that no actual contact takes place); cohesion as a balance between attraction and repulsion in the shortest range; ‘fermentation’ (i.e., broadly speaking, chemical processes involving a transformation of one substance into another through the release of air from solids or liquids), and electricity and magnetism in the intermediate range, where both repulsive and attractive behaviors manifest themselves” (ibid., pp. xiii-xiv). The first part of De viribus vivis is devoted to an analysis of the famous vis viva controversy. During the period 1676-89, Leibniz had proposed that the “living force” of a mechanical system is conserved, in opposition to Descartes and Newton who maintained that it was total momentum that is conserved. Madame du Châtelet developed Leibniz’s ideas and showed that “living force” depends on the square of the velocity. “Although the 1743 edition of d’Alembert’s Traité [de Dynamique] had been cited by many authors as resolving the dispute, it provided little more clarification than contrasting dead with living forces and calling the argument a ‘dispute over words’ … Although the 1758 edition of the Traité did point out that momentum could be considered as a force acting during a given time, and vis viva as a force acting over the space traversed, d’Alembert was anticipated in this insight by Roger Boscovich. Pierre Costabel has shown that Boscovich’s De Viribus Vivis (Rome, 1745) suggested a separate graphical representation for each of the two measures of force. The De Viribus Vivis is a fifty-page work of difficult Latin dealing with two separate subjects involving living force. According to Costabel it shows that Boscovich possessed a very thorough understanding of the history of the quarrel before his own intervention, from Leibniz and Bernoulli to Voltaire, de Mairan and du Châtelet … “Although not explicitly stated, Boscovich’s analysis contains the necessary elements for distinguishing force, mv, as a time-dependent function and mv2 as a space-dependent function. It brings together aspects of force analysed previously by Bernoulli, Louville and others. On the question of elastic and inelastic collisions briefly discussed in his paper, Boscovich used the principle of action and reaction and its equivalent, the conservation of quantity of motion taken in an algebraic sense. In verifying the conservation of living force in the sense of Leibniz he said that living force, being formed as it is by the square of the velocity, destroys the sign of that velocity, whereas the quantity of motion conserves all its characteristic elements. Boscovich concludes in paragraph 39 of De Viribus Vivis that the question of living force is a question of language and completely useless. In spite of this analysis of ‘force’, however, Boscovich believed that momentum was the true measure of force, vis viva being valid only as a method of calculation. In his De Viribus Vivis as well as in his later Philosophiae Naturalis Theoria (1758), he argued that there were no living forces in nature” (Iltis, pp. 138-140). De viribus was reprinted in 1747 in Commentariis Academiae Bononiensis, vol. 2, pars 3, §§21-49. Boscovich was born on 18 May 1711 in Dubrovnik, now in Croatia, then an independent city-state surrounded by the Ottoman Empire and the Venetian Republic. There is some ambiguity about how to write Boscovich’s name. In English he is usually referred to as Roger Joseph Boscovich, in Italian as Ruggiero Giuseppe Boscovich, while in his native Croatian he is called Ruder Josip Boškovic. His surname is derived from the word Boško, which in Croatian means “little God”. “This Croatian physicist, mathematician, and astronomer is considered the last great polymath. Educated first at the Jesuit College in his native Dubrovnik, he entered the novitiate in Rome in 1725 and later attended the Collegium Romanum, beginning to teach mathematics there in 1740. A corresponding member of the Academy of Sciences at Paris, he travelled there in 1759. The following year he travelled to London, where he met Benjamin Franklin and was elected F.R.S.; he then travelled widely throughput Europe and Eastern Europe. On his return to Italy in 1763, he was elected to the chair of mathematics at Pavia, where he reorganized the department with an emphasis on applied mechanics, and also played a leading role in organizing the observatory at Brera. In 1772 his connection with the observatory was terminated, and, in response, he resigned his professorship; the Jesuit order was suppressed in the following year. At the urging of friends, he removed to Paris, but returned to Italy in 1782 to prepare the manuscripts for his Opera. His scientific interests were divided between astronomy, optics, geodesy, and mathematics, mechanics, and natural philosophy. As well as his religious and teaching duties, Boscovich undertook several practical and diplomatic commissions for both secular and ecclesiastical authorities” (Roberts & Trent, p. 43). Boscovich died of pneumonia on 13 February 1787 in Milan, and was quietly buried at Santa Maria Padone. PMM 203 (for Theoria); Riccardi I.1 174 n 21; Sommervogel I 1832 n 22. Guzzardi, Ruggiero Boscovich’s Theory of Natural Philosophy, 2020. Iltis, ‘D’Alembert and the vis viva controversy,’ pp. 135-144 in Studies in History and Philosophy of Science, Part A, 1 (1970); Jammer, Concepts of Force, 1962. Kragh, Higher Speculations: Grand Theories and Failed Revolutions in Physics and Cosmology, 2011; Whyte (ed.), Roger Joseph Boscovich, S.J., F.R.S., 1711-1787: Studies of His Life and Work on the 250th Anniversary of His Birth, 1961.
4to (242 x 178mm), pp. XLIX, [1, blank], folding table with diagrams appended as extension of last leaf, printer’s device on title, ornamental woodcut and decorative initial at beginning of text (very light browning and foxing, manuscript correction to p. IX as in other copies). Contemporary gilt brocade paper wrappers (a few small stains on covers, spine rubbed). An excellent copy.
Item #5520
Price: $12,500.00