The chemical basis of morphogenesis. Offprint from: Philosophical Transactions of the Royal Society of London, Series B, Vol. 237, No. 641, 14 August, 1952.
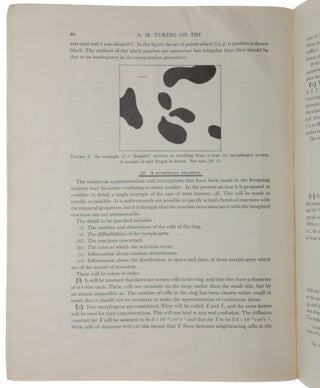
London: Cambridge University Press for the Royal Society, [1952]. First edition of the extremely rare true offprint (without price to front wrapper), of Turing’s last major published work, which was “in every respect ahead of its time” (Copeland, p. 510). Taking his cue from the zoologist D’Arcy Thompson, who held that the forms of living things are to be explained in terms of the operation of physical forces and mathematical laws, Turing presents here the first mathematical theory of embryology. “At a time when Crick and Watson were using X-ray diffraction to establish the structure of DNA, Turing was grappling with a theoretical understanding of how information might be spread and diffused at a chemical level. In a classic statement of the scientific method Turing wrote: ‘a mathematical model of the growing embryo will be described. This model will be a simplification and an idealisation, and consequently a falsification. It is to be hoped that the features retained for discussion are those of greatest importance in the present state of knowledge’. The result was applied mathematics par excellence. Just as the simple idea of the Turing machine had sent him into fields beyond the boundaries of Cambridge mathematics, so now this simple idea in physical chemistry took him into a region of new mathematical problems” (Hodges, p. 434). “Alan Turing’s paper, ‘The chemical basis of morphogenesis,’ has been hugely influential in a number of areas. In this paper, Turing proposed that biological pattern formation arises in response to a chemical pre-pattern which, in turn, is set up by a process now known as diffusion-driven instability. The genius of this work was that he considered a system which was stable in the absence of diffusion and then showed that the addition of diffusion, which is naturally stabilising, actually caused an instability. Thus, it was the integration of the parts that was as crucial to the understanding of embryological development as the parts themselves – patterns emerged or self-organised as a result of the individual parts interacting. To see how far ahead of his time he was, one has to note that it is only now in the post-genomic era of systems biology that the majority of the scientific community has arrived at the conclusion he came to 60 years ago … Applications of Turing’s work to developmental biology are too numerous to list but include limb development, pigmentation patterning, hair and feather germ formation, tooth morphogenesis, phyllotaxis, hydra patterning and regeneration. Moreover, ideas of self-organization now abound in biology, chemistry and ecology. The stimulus for a lot of this work stems from Turing’s original ideas... Although still very controversial, Turing’s theory for morphogenesis provided a paradigm shift in our way of thinking” (Maini, in Alan Turing: his work and impact, p. 684). There are two separate issues of ‘The chemical basis of morphogenesis’, the genuine author’s presentation offprint offered here, and a commercially produced reprint; the latter differs from the former only in the presence of a price (eight shillings) at the foot of the front wrapper. ABPC/RBH records the sale of only one copy of this offprint (Christie’s, June 12, 2013, lot 136, £13,125) Provenance: Owner’s name written in ink to upper right corner of front wrapper; botanist Otto L. Stein (1925-2014). The offprint is accompanied with a signed typed letter from 1956 by R.A. Brooker at the Computing Machine Laboratory Manchester in reply to Stein’s request to Turing for a copy of the offprint. “Alan had thought about embryology all the time, fascinated by the fact that how such growth was determined was something ‘nobody has yet made the smallest beginnings at finding out.’ There had been little advance since Growth and Form [by D’Arcy Thomspon], the 1927 classic that he had read before the war... “The greatest puzzle was that of how biological matter could assemble itself into patterns which were so enormous compared to the size of the cells. How could an assemblage of cells ‘know’ that it must settle into a five-fold symmetry, to make a starfish? How could the Fibonacci pattern of a fir-cone be imposed in its harmonious, regular way upon a growing plant? How could matter take shape or, as biological Greek had it, what was the secret of morphogenesis? Suggestive words like ‘morphogenetic field’, vague as the Life Force, were employed by biologists to describe the way that embryonic tissue seemed to be endowed with an invisible pattern which subsequently dictated its harmonious development. It had been conjectured that these ‘fields’ could be described in chemical terms – but there was no theory of how this could be. Polanyi believed that there was no explanation except by a guiding esprit de corps; the inexplicability of embryonic form was one of his many arguments against determinism. Conversely, Alan told Robin [Gandy] that his new ideas were intended to ‘defeat the Argument from Design’... “There were other suggestions in the literature for the nature of the ‘morphogenetic field’, but at some point Alan decided to accept the idea that it was defined by some variation of chemical concentrations, and to see how far he could get on the basis of that one idea... [The problem was] to discover circumstances in which a mixture of chemical solutions, diffusing and reacting with each other, could settle into a pattern, a pulsating pattern of chemical waves; waves of concentration into which the developing tissue would harden; waves which would encompass millions of cells, organising them into a symmetrical order far greater in scale... “There was one central, fundamental problem. It was exemplified in the phenomenon of gastrulation... in which a perfect sphere of cells would suddenly develop a groove, determining the head and tail ends of the emergent animal. The problem was this: if the sphere were symmetrical, and the chemical equations were symmetrical, without knowledge of left or right, up or down, where did the decision come from? “To examine this moment of crisis mathematically, one had to approximate over and over again. He had to ignore the internal structure of the cells, and forget that the cells themselves would be moving and splitting as the patterning process took place... But with these reservations, his approach was to take the model and try it out... The result was applied mathematics par excellence. Just as the simple idea of the Turing machine had sent him into fields beyond the boundaries of Cambridge mathematics, so now this simple idea in physical chemistry took him into a region of new mathematical problems... “[On 12 February 1951] the Ferranti Mark I computer was delivered at the Manchester department, which by now had a newly built Computing Laboratory to house it. Alan wrote to Mike Woodger back at the [National Physical Laboratory]: ‘Our new machine is to start arriving on Monday. I am hoping as one of its first jobs to do something about ‘chemical embryology’. In particular I think one can account for the appearance of Fibonacci numbers in connection with fir-cones’. It had been twenty-one years, and the computer had come of age. It was as though all that he had done, and all that the world had done to him, had been to provide him with an electronic universal machine, with which to think about the secret of life” (Hodges, pp. 430-437). “During the final years of his life Turing was working on what would now be called Artificial Life or A-Life. He used the Ferranti Mark I computer belonging to the Manchester University Computing Machine Laboratory to simulate a chemical mechanism by which the genes of a zygote may determine the anatomical structure of the resulting animal or plant. He described these studies as ‘not altogether unconnected’ to his work on neural networks, as ‘brain structure has to be ... achieved by the genetical embryological mechanism, and this theory that I am now working on may make clearer what restrictions this really implies.’ During this period Turing achieved the distinction of being the first to engage in the computer-assisted exploration of non-linear dynamical systems” (Copeland on alanturing.net). Claude Shannon (1916-2001) is known as ’the founder of information theory’ for his landmark paper ‘A mathematical theory of communication’ (1948), and for his thesis, ‘A symbolic analysis of relay and switching circuits’ (1936), which founded the theory of digital circuit design on the basis of Boolean algebra. “Shannon, who died in February after a long illness, was one of the greatest of the giants who created the information age. John von Neumann, Alan Turing and many other visionaries gave us computers that could process information. But it was Claude Shannon who gave us the modern concept of information – an intellectual leap that earns him a place on whatever high-tech equivalent of Mount Rushmore is one day established” ” (‘Claude Shannon: reluctant father of the digital age,’ MIT Technology Review, July 1, 2001). Shannon and Turing were in contact for two months early in 1943. Turing had been posted to Washington to share with the U.S. Navy’s cryptanalytic service the methods used by the British Government Code and Cypher School at Bletchley Park to break the ciphers used by the Kriegsmarine U-boats in the North Atlantic Ocean. He was also interested in the encipherment of speech and to this end spent time at Bell Labs. Shannon and Turing met at teatime in the cafeteria. Turing showed Shannon his 1936 paper that defined what is now known as the ‘Universal Turing machine’. This impressed Shannon, as many of its ideas complemented his own. In 1956 Shannon considered the problem of finding the smallest p[ossible universal Turing machine. In ‘A universal Turing machine with two internal states’ (pp. 157-165 in Automata Studies, Shannon & McCarthy, eds.), Shannon showed that a universal Turing machine can be constructed with a single tape and only two internal states, provided that enough tape symbols are used; and, conversely, that two tape symbols are sufficient provided there are enough internal states. Offprints of Turing’s papers are extremely rare in institutional holdings, and even more so in commerce. We have located only the copy in the Turing Archive at King’s College, Cambridge and that in the Max Newman collection (now at Bletchley Park). B. J. Copeland, The Essential Turing, Clarendon Press, 2004; Andrew Hodges, Alan Turing: The Enigma, 1983.
Large 4to (302 x 233 mm), original light brown printed wrappers, light wear to extremities, otherwise fine and unrestored. Internally with notes and markings (most likely by Stein).
Item #5612
Price: $36,500.00